
- •С.В. Шапиро Курс физики Учебное пособие
- •Рецензенты:
- •Содержание
- •Раздел 1. Механика……………………………………...……….………………..8
- •Раздел 2. Термодинамика..……………………………………………………...45
- •Раздел 3. Электричество и магнетизм………………………………………...86
- •Раздел 5. Физические основы строения материи…………………………..175
- •Цель и задачи курса
- •Раздел первый. Механика глава первая. Кинематика
- •1.1. Материальная точка и основные характеристики ее движения
- •Декартовой системе координат
- •1.2. Вращательное движение материальной точки
- •Векторное изображение угловой скорости (б)
- •1.3. Кинематика твердого тела. Разложение произвольного движения на поступательное и вращательное
- •1.4. Относительное движение
- •1.5. Релятивистские эффекты в кинематике
- •Масштаба длины (в)
- •Вопросы по первой главе:
- •Глава вторая. Динамика
- •2.1. Взаимодействие материальных точек. Понятие силы
- •2.2. Законы статики изолированного множества материальных точек
- •1 Закон статики.
- •2 Закон статики.
- •2.3. Закон сохранения импульса изолированного множества материальных точек. Центр масс
- •2.4. Закон сохранения момента импульса изолированного множества материальных точек. Теорема Штейнера
- •2.5. Работа, энергия, закон сохранения энергии
- •Материальной точки Mq: а, б – под действием одной материальной точки Mp;
- •2.6. Взаимодействие двух изолированных множеств материальных точек
- •2.7. Связи абсолютно-твердых тел
- •2.8. Релятивистская масса
- •2.9. Гравитационное взаимодействие
- •2.10. Динамика упругого тела
- •Вопросы по второй главе:
- •Раздел II. Термодинамика глава третья. Идеальный газ
- •3.1. Основные характеристики идеального газа
- •Движением всех корпускул, входящих в газ (а), их упорядоченным движением (б) и в промежуточной ситуации (в)
- •3.2. Уравнение состояния Менделеева–Клапейрона
- •3.3. Работа идеального газа. Теплота и внутренняя тепловая энергия. Первый закон термодинамики
- •3.4. Энтропия. Второй принцип термодинамики
- •Аналогично для второго газа записываем
- •Если принять отношения
- •3.5. Адиабатические, изотермические, изохорические, изобарические процессы
- •3.6. Неравновесные системы
- •При теплообмене: 1 – источник тепловой энергии; 2 – приемник тепловой энергии (холодильник); 0 – объем идеального газа (открытая система)
- •Риc. 3.7. К раcчёту процесса преобразования теплового движения в упорядоченное в простейшей неравновесной системе
- •3.7. Цикл Карно
- •3.8. Распределение молекул газа по скоростям
- •Вопросы по третьей главе:
- •Глава четвёртая. Реальный газ и основы кинетики газа
- •4.1. Уравнение Ван дер-Ваальса
- •4.2. Столкновения молекул. Средняя длина свободного пробега. Скорость дрейфа
- •При столкновении корпускул идеального газа
- •Модель движения материальной точки под действием постоянной силы в условиях дескретно – повторяющегося столкновения с препятствиями (б) и зависимость V(τ) для такого движения
- •4.3. Явления переноса в газе
- •4.4. Диффузия газов
- •4.5. Теплопроводность
- •4.6. Внутреннее трение в газах (вязкость)
- •4.7. Основы аэро- и гидродинамики. Возникновение вихрей
- •В сплошной среде (б, в)
- •Вопросы по четвертой главе:
- •Раздел третий. Электричество и магнетизм глава пятая. Электростатика
- •5.1. Закон Кулона
- •Электрического взаимодействия; б – воздействие (n-1) зарядов на заряд qN;
- •5.2. Электрическое поле и его основные характеристики
- •И эквипотенциальными поверхностями (а) и поток вектора напряженности через инфинитезимальную поверхность (б)
- •5.3. Теорема Гаусса–Остроградского
- •5.4. Примеры применения теоремы Гаусса–Остроградского
- •Бесконечной длины: а – выбор замкнутой поверхности;
- •5.5. Электростатическое поле в диэлектрике
- •5.6. Электростатическая индукция. Теорема Гаусса-Остроградского для поля в разнородной среде
- •В разнородной среде
- •5.7. Энергия электростатического поля
- •Вопросы по пятой главе:
- •Глава шестая. Магнетизм
- •6.1. Взаимодействие движущихся зарядов и проводников с токами
- •С движущимися электронами; б – иллюстрация закона Био-Савара-Лапласа
- •6.2. Основные характеристики магнитного поля.
- •6.3. Закон полного тока
- •Магнитное поле торроидальной катушки
- •6.5. Электромагнитная индукция
- •Наводимого электромагнитной индукцией потока
- •6.6. Пара-, диа- и ферромагнетики
- •6.7. Явление взаимоиндукции. Идеальный трансформатор
- •Его схематическое изображение (б)
- •6.8. Энергия магнитного поля
- •Вопросы по шестой главе:
- •Глава седьмая. Электрический ток
- •7.1. Основные элементы цепи постоянного тока. Законы Ома и Джоуля–Ленца
- •7.2. Законы Кирхгофа для разветвленной цепи
- •(К описанию законов Кирхгофа)
- •7.3. Переменный синусоидальный ток
- •Векторами: а – единичный вектор во вращающейся системе координат;
- •7.4. Переменная синусоидальная эдс. Законы Ома и Кирхгофа в комплексном виде
- •И участок цепи синусоидального тока (в)
- •7.5. Переходные процессы в электрических цепях
- •Вопросы по седьмой главе:
- •Глава восьмая. Электромагнитное поле
- •8.1. Уравнения Максвелла
- •8.2. Теорема Умова–Пойнтинга
- •Двухпроводной линии (а) и круглого провода (б)
- •8.3. Плоское электромагнитное поле в диэлектрике
- •Плоской электромагнитной волны в диэлектрике
- •П(х); г – формирование е0(х)
- •8.4. Плоское синусоидальное электромагнитное поле в диэлектрике
- •8.5. Плоская электромагнитная волна в проводящей среде
- •8.6. Плоское синусоидальное электромагнитное поле в смешанной среде
- •8.7. Сферическое электромагнитное поле в диэлектрике
- •Вопросы по восьмой главе:
- •Для выбора основных цветов:1 – красный;2 – зелёный;3 – синий
- •9.2. Интерференция света
- •Монохроматических волн; в – интерференция сферических волн
- •Предмета на фотоплёнку при облучении его лазером (монохроматическим когерентным светом;б)получение объёмного (стереоскопического) изображения этого предмета
- •9.3. Дифракция света
- •9.4. Отражение и преломление волн на границе двух сред
- •9.5. Геометрическая оптика
- •Вопросы по девятой главе:
- •Глава десятая. Акустика
- •10.1. Акустические волны в газе. Волновое уравнение
- •10.2. Поперечные упругие колебания протяжённых твердых тел и поверхностей жидкостей
- •10.3. Распространение гармонического звука в газе
- •10.4. Негармонические звуковые колебания
- •Вопросы по десятой главе:
- •Раздел пятый. Физические основы строения материи глава одиннадцатая. Элементы квантовой механики
- •1.1. Принцип неопределенности
- •11.2. Волна вероятности. Уравнение Шредингера
- •Вероятность её нахождения вдоль оси X(б)
- •11.3. Волна вероятности ускоряющейся частицы. Волновой пакет
- •При ускорении частицы (а) и его структура (б)
- •11.4. Движение электрического заряда в центрально-симметричном электрическом поле
- •А) при числе эпициклов,равном 1; б) при числе 2
- •Вопросы по одиннадцатой главе:
- •Глава двенадцатая. Физические основы строения материи
- •12.1. Элементарные частицы
- •Камере в результате столкновения π ––мезона с протоном р(а). В результате реакции появились k0 – мезон и λ0 – гиперон.Они на фотографии
- •12.2. Модели ядра
- •12.3. Ядерные процессы
- •12.4. Структура атома. Энергетические уровни
- •12.5. Некоторые физические явления, обусловленные квантовыми процессами в атомах
- •12.6. Формирование молекулярных структур
- •Атомов от расстояния между их центрами
- •12.7. Агрегатные состояния вещества
- •12.8. Твердое тело
- •Двух молекул от расстояния между ними
- •В кристаллах
- •Вопросы по двенадцатой главе:
- •Приложения
- •Примеры решения задач Несколько советов
- •Несколько предварительных замечаний
- •1. Кинематика.
- •2. Статика Задача № п.2
- •Решение
- •3. Динамика Задача № п.3
- •Решение
- •4. Термодинамика Задача№ п.4
- •Решение
- •5. Электростатика Задача № п.5
- •Решение
- •6. Магнитное поле Задача № п.6
- •Решение
- •7. Электрический ток Задача № п.7
- •Решение
- •8. Переменное электромагнитное поле Задача № п.8
- •Решение
- •9. Акустика Задача № п.9
- •Решение
- •10. Оптика Задача № п.10
- •Решение
- •11. Атомная и ядерная физика Задача № п.11
- •Решение
- •12. Молекулы и кристаллы Задача № п.12
- •Решение
- •Некоторые сведения из векторного анализа
- •Международная система единиц
- •3.1. Основные единицы и их эталоны
- •3.2. Единицы механических величин
- •П.3.3. Единицы тепловых величин
- •3.4. Единицы электромагнитных величин.
- •3.5. Единицы электромагнитного излучения и освещенности
- •Основные хронологические даты истории физики
- •Приложение 5 основные физические константы
- •Список литературы
- •Шапиро Семен Валентинович
- •450078, Г. Уфа, ул. Чернышевского, 145, к. 206; тел. (347) 241-69-85.
6.6. Пара-, диа- и ферромагнетики
До сих пор в этой главе рассматривалось магнитное поле в вакууме, т.е. в среде, лишенной каких-либо микроисточников магнитного поля. Реально все вещества состоят из атомов, которые содержат подвижную электронную оболочку. Отрицательно заряженные электроны совершают два вида движения – относительно ядра и относительно траектории этого первого движения. В какой-то степени можно провести аналогично с движением Земли – вращение по орбите вокруг Солнца и вращение вокруг собственной оси. Однако на самом деле все в атоме гораздо сложнее и использовать данную модель для расчетов не представляется возможным.
Все детали строения
материи на микроуровне и уточненный
расчет их влияния на магнитное поле
будет рассмотрен в четвертом разделе
книги. Здесь же мы представим среду
заполненной большим количеством
маленьких контуров с током – рисунок
6.9, а. Каждый контур на этом рисунке
снабжен вектором
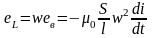 ,
именуемым магнитным моментом.
Такое название он приобрел по аналогии
с электрическим моментом диполя
,
именуемым магнитным моментом.
Такое название он приобрел по аналогии
с электрическим моментом диполя
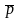 (см. § 5.6).
(см. § 5.6).
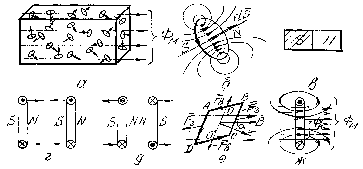
Рис. 6.9. К описанию магнитного поля в материальной среде:
а – общий случай расположения магнитных контуров в веществе;
б – магнитное поле кругового контура тока; в – эквивалентный магнит;
г, д – силовое взаимодействие контуров с согласным и встречным направлением. тока; е – поворот контура с током во внешнем магнитном поле;
ж – суммирование поля контура с внешним магнитным полем
Действительно, если на контур тока i мысленно натянуть мыльную пленку, то магнитные силовые линии с одной стороны в нее входят, а с другой – выходят – рисунок 6.9, б. Ту сторону контура, в которую силовые линии входят, именуют южным полюсом – S, а из которых выходят – северным – N.
Иными словами, контур тока можно представить магнитным диполем – рисунок 6.9, в.
Если подвести два контура друг к другу так, чтобы токи в них были направлены в одинаковую сторону – рисунок 6.9, г, то они будут притягиваться друг к другу – см. § 6.1.
При этом северный полюс первого контура соприкасается с южным контуром второго. Налицо полная аналогия с двумя электрическими диполями, которые также притягиваются друг к другу, когда соприкасается положительный заряд одного диполя с отрицательным другого.
Наоборот, когда два магнитных контура соприкасаются одинаковыми полюсами – рисунок 6.9, д, они отталкиваются.
Ясно, что аналогия взаимодействия контуров с током и диполей чисто феноменологическая, однако ей удобно пользоваться при объяснении макроэффектов.
Магнитный момент равен
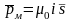 ,
(6.21)
,
(6.21)
где
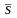 – вектор площади, охваченный контуром
с током i
(рис.6.9, б). Направление
и
такое, чтобы с конца их векторов i
был виден текущим против часовой стрелки.
– вектор площади, охваченный контуром
с током i
(рис.6.9, б). Направление
и
такое, чтобы с конца их векторов i
был виден текущим против часовой стрелки.
Если контур с током пронизывается магнитным потоком, силовые линии которого образуют с вектором угол α, возникает пара сил, стремящаяся повернуть этот контур так, чтобы угол α стал равен нулю.
Легче
всего рассчитать эту пару, если принять
конфигурацию контура в виде прямоугольника
– рисунок 6.9, е. Горизонтальные силы
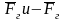 ,
действующие на боковые стороны контура
AD и ВС,
взаимоуравновешиваются. Вертикальные
силы
,
действующие на боковые стороны контура
AD и ВС,
взаимоуравновешиваются. Вертикальные
силы
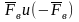 образуют момент
образуют момент
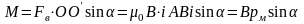 (6.22, а)
(6.22, а)
или, в векторной форме
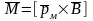 (6.22, б)
(6.22, б)
Эта формула справедлива для контуров любой конфигурации.
После завершения
поворота контура, т.е. тогда, когда вектор
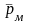 совпадает с вектором
совпадает с вектором
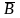 по
направлению, магнитный поток контура
по
направлению, магнитный поток контура
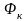 будет складываться с внешним потоком
ФМ внутри площадки
- рисунок 6.7, ж.
будет складываться с внешним потоком
ФМ внутри площадки
- рисунок 6.7, ж.
Из этого можно было бы заключить, что при воздействии магнитного поля на среду, состоящую из микроконтуров с током, все они повернутся поперек силовых линий и своими полями усилят внешнее поле. Однако на самом деле этого не происходит по следующим причинам.
1. Контуры совершают тепловое (хаотическое) движение, постоянно соударяясь друг с другом произвольным образом. Эти соударения разрушают любой возможный порядок, в том числе и указанный выше.
2. Электроны,
движение которых рассматривается как
контур тока i,
обладают не только зарядом (-е),
но и массой me=9,11·10-31
кг. Поэтому контур i
обладает не только магнитным моментом
,
но и механическим
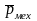 ,
т.е. напоминает волчок (рис. 6.10).
,
т.е. напоминает волчок (рис. 6.10).
Если попытаться
повернуть ось волчка вокруг перпендикуляра
к этой оси, то возникает её новое вращение,
именуемое прецессией [3]. В
результате электрон оказывается вовлечен
в два вида вращения – вокруг своей
собственной оси и оси прецессии. Магнитный
момент этого второго вращения
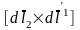 (см.
рис. 6.9) в значительной степени ослабляет
действие момента
.
У разных материалов соотношение
и
разное. Если
>
,
то магнитное поле контуров среды
ослабляет внешнее поле, а если
<
,
то усиливает.
(см.
рис. 6.9) в значительной степени ослабляет
действие момента
.
У разных материалов соотношение
и
разное. Если
>
,
то магнитное поле контуров среды
ослабляет внешнее поле, а если
<
,
то усиливает.
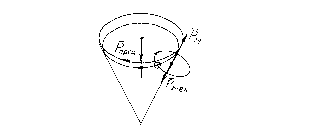
Рис. 6.10. К возникновению диамагнетизма
Во всяком случае, и в том, и в другом случае магнитное поле меняется под действием среды незначительно – от тысячных долей до единиц процента.
Среда, усиливающая внешнее магнитное поле, именуется парамагнетиком, а ослабляющая – диамагнетиком.
Количественно
изменение магнитного поля под воздействием
среды характеризуется относительной
магнитной проницаемостью
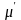 .
Во всех формулах этой главы для величин
B,
F,
Ф,
Gм,
Rм,
L
следует заменять
на произведение
.
Во всех формулах этой главы для величин
B,
F,
Ф,
Gм,
Rм,
L
следует заменять
на произведение
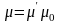 (6.23)
(6.23)
Так же, как и в
случае электростатического поля, для
того, чтобы исключить из формул зависимость
от свойств среды, вводится расчетная
величина, не зависящая от
.
Такой величиной является напряженность
магнитного поля
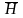 ,
равная
,
равная
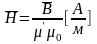 (6.24)
(6.24)
Подставляя (6.24) во все формулы этой главы, расчетчик магнитных цепей окажется освобожден от влияния параметров среды на результаты его расчетов. В частности, закон полного тока в магнитной среде с зависящей от координат величиной имеет вид
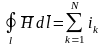 (6.25)
(6.25)
где все входящие в формулу величины, кроме , те же самые, что и в (6.12).
Особыми свойствами обладают среды, именуемые ферромагнетиками. В этих средах атомы расположены так, что их магнитные моменты направлены в одну и ту же сторону. Участки вещества с такими однонаправленными магнитными моментами именуются доменами (рисунок 6.11, а). Без воздействия внешнего магнитного поля эти домены расположены хаотически друг относительно друга и их поля взаимно компенсируют друг друга.
Типичным представителем ферромагнетиков является железо и его многочисленные сплавы.
Домены условно можно представить магнитиками с северным и южным полюсом – рисунок 6.11, б. При воздействии внешнего поля эти магнитики поворачиваются вдоль него, и их поля добавляются к его потоку Фвн. На рисунке 6.11, б внешнее поле создается катушкой с током i. С увеличением i растет напряженность внешнего поля .
Магнитное поле,
создаваемое доменами, значительно
больше внешнего, поэтому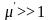 .Для
современных ферромагнитных материалов
эта величина колеблется в пределах от
102
до 105.
.Для
современных ферромагнитных материалов
эта величина колеблется в пределах от
102
до 105.
Проследим, как изменяется результирующая магнитная индукция В в ферромагнетике рисунок 6.11, б от напряженности Н (рисунок 6.11, в).
С ростом Н
от 0
до Нк
происходит крутой рост величины В,
обусловленный поворотом магнитиков в
направлении
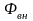 .
Этот участок именуется зоной возбуждения.
После того, как все магнитики повернулись
в направлении поля, магнитная индукция
растет лишь за счет увеличения внешней
составляющей:
.
Этот участок именуется зоной возбуждения.
После того, как все магнитики повернулись
в направлении поля, магнитная индукция
растет лишь за счет увеличения внешней
составляющей:
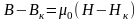 .
(6.26)
.
(6.26)
Величина Нк и соответствующая ей Вк характеризуют собой колено кривой намагничивания. Рост поля при Н>Нк осуществляется с малым наклоном, т.е. так же, как в вакууме. Этот участок именуется зоной насыщения. Если теперь уменьшать Н, то зависимость В(Н) пойдет по совсем другой кривой.
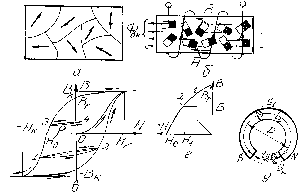
Рис. 6.11. Ферромагнитные явления: а – произвольное расположение доменов;
б – поворот доменов во внешнем магнитном поле; в – полные и частные циклы гистерезиса; г – кривая возврата постояного магнита;
д – торроидальный постоянный магнит
Это связано с тем, что магнитики, расположившись упорядоченно, друг относительно друга, вовсе не собираются вновь разрушать этот порядок.
И лишь после того, как ток в катушке, а вместе с ним и конец вектора Н, сменят свое направление, магнитики начнут переворачиваться, сначала вновь располагаясь хаотически, а затем ориентируясь противоположно первоначальному. Напряженность Нс, при которой индукция в ферромагнетике равна нулю, именуется коэрцитивной силой.Далее процесс повторяется. Кривая, описываемая изображающей точкой в координатах В(Н) – см. рисунок 6.11, в, – именуется петлей гистерезиса.
В том случае, когда процесс размагничивания прекратится при напряженности Н > -Нс, а затем начнется намагничивание (т.1 на рисунке 6.11, в), изображающая точка кривой В(Н) начнет двигаться по кривой возврата 1-2 до правой ветви петли гистерезиса, а затем так же, как в описанном выше нормальном процессе перемагничивания. Впрочем, если процесс перемагничивания, начавшийся при Н>-Нс, не дойдет до правой ветви гистерезиса, а вновь будет характеризоваться уменьшением Н (кривая 3-4), зависимость В(Н) опишет малую петлю, именуемую петлей возврата.
В зависимости от величины Нс все ферромагнетики делятся на магнитомягкие (Нс не более 100А/м) и магнитотвердые (Нс более 10000А/м). Первые используются в различных электротехнических устройствах с переменным магнитным потоком, когда влияние петли гистерезиса нужно свести к минимуму. Вторые, наоборот, в тех устройствах, которые принципиально основаны на использовании гистерезисных свойств ферромагнитной среды. В частности, для изготовления постоянных магнитов.
Принцип действия постоянных магнитов основан на использовании участка (Вr,-Нс) петли гистерезиса (см. рисунок 6.11, в).
Рассмотрим
постоянный магнит (рисунок 6.11,д.). Он
представляет собой тор сечением S1
и диаметром средней линии D
(D>>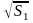 ),
в котором выполнен воздушный зазор
длиной
),
в котором выполнен воздушный зазор
длиной
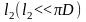 .
.
Согласно закону полного тока (6.25) зависимость напряженностей магнитного поля внутри ферромагнетика Н1 и в зазоре Н2 друг от друга следующая
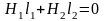 .
(6.27, а)
.
(6.27, а)
Зависимость
между индукцией внутри магнита В1
и в зазоре В2
определим, учитывая, что магнитный
поток Фм
одинаков и внутри сердечника и в
зазоре. Одновременно допускаем, что
силовые линии в зазоре идут по
концентрическим вокруг оси тора
окружностям, т.е. также, как в зазоре.
Такое допущение тем точнее, чем меньше
длина зазора
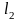 ,
чем
,
чем
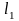 .
Получаем
.
Получаем
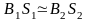 (6.27,
б)
(6.27,
б)
или
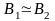 ,
(6.27, в)
,
(6.27, в)
так
как
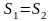 .
.
Подставляя (6.27, в) в (6.27, а), имеем
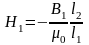 .
(6.27, г)
.
(6.27, г)
Зависимость (6.27,г) представляет собой прямую линию 2, проходящую в левом квадранте В(Н) (см. рисунок 6.11, г). В этом же квадранте лежит участок размагничивания петли гистерезиса 1.
На их пересечении и лежат истинные значения индукции и напряженности магнитного поля постоянного магнита.
