4.7. Основы аэро- и гидродинамики. Возникновение вихрей

Во всех предшествующих параграфах этого раздела газ рассматривается как большое скопление молекул – микроскопических частиц, хаотически двигающихся и соударяющихся друг с другом. Однако газ можно рассматривать и как сплошную среду, отдельные участки которой могут свободно или с небольшим трением перемещаться друг относительно друга. В этом случае газ аналогичен жидкости. Поэтому все соотношения, справедливые для газа, как сплошной среды, верны и для жидкости. На рис. 4.7, а изображен объем газа, в котором выделен инфинитезимальный шар радиуса dr. Первой особенностью газа, как сплошной среды, является независимость величины давления на поверхность шара 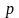от направления. О том, что давление газа во все стороны одинаково, мы можем судить хотя бы по тому, что надуваемый резиновый объем при отсутствии дефектов и неровностей принимает форму сферы. Вторая особенность газа заключается в том, что ускорение микрообъема этого газа под действием внешних сил (например, силы тяготения) и внутренних, т.е. давления окружающих этот микрообъем участков, является производной его скорости не только по времени, но и по пространственным координатам.

На рисунке 4.7, б изображен путь движения выбранного микро -объема внутри газа. Точки 1 и 2 отстают друг от друга на бесконечно малый участок пути . Ускорение этого микрообъема равно

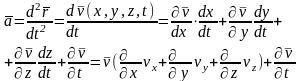(4.18,а)

Выражение, стоящее в скобках, можно представить скалярным произведением двух векторов:

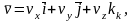(4.18,б)

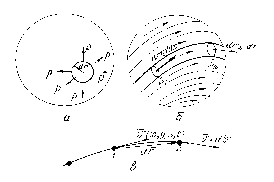
Рис. 4.7. К расчету давления (а) и скоростей перемещения масс

В сплошной среде (б, в)

где - векторный оператор дифференцирования, именуемый оператором Гамильтона. В математическом курсе векторного исчисления доказывается, что с этим оператором можно обращаться как с обычным вектором, в частности , умножать на обычные вектора скалярно (скалярное произведение) и векторное (векторное произведение). С учетом этого записываем

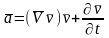. (4.18, в)

С другой стороны, согласно второму закону Ньютона (см. § 2.2), ускорение

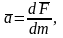(4.18, г)

где - масса микрообъема , а - действующая на него сила. Эта сила складывается из трех составляющих

(4.18, д)

где - суммарная сила давления внешних слоев газа на поверхность микрообъема, - напряженность поля тяготения Земли в точке, где находится микрообъем, 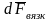- сила вязкого трения микрообъема о соседние слои газа. Величина

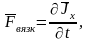(4.18, е)

где 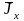- определяется из (4.16, г), а из закона Всемирного тяготения:

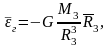(4.18, ж)

где 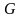- гравитационная постоянная, равная 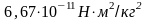, - масса Земли, равная, _, R₃ – величина радиуса поверхности Земли, равная , – радиус-вектор из центра Земли в данную точку гравитационного поля.

Из (4.18, в) ÷ (4.18, ж) получаем

. (4.19)

Соотношение (4.18, в) можно преобразовать, учитывая следующую формулу векторного анализа [5]:

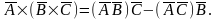
Используя эту формулу, имеем

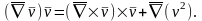
где знак «×» - знак векторного произведения. Подставляя в (4.18,г) и учитывая (4.19), имеем

, (4.20)

где

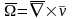(4.21)

– циркуляция вектора скорости вокруг бесконечно малой петли. Первое слагаемое правой части свидетельствует о том, что при определенных условиях в газе возникает вихревое (круговое) движение, хотя действующие на него силы вращающего момента не имеют. Именно этим объясняется появление смерча в воздухе при ураганах, закручивание жидкости при вытекании ее из сосуда (например, ванны) через небольшое отверстие. Этой же причиной объясняется возникновение турбулентного течения жидкости.