3.6. Неравновесные системы
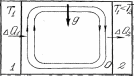
Вновь рассмотрим объем идеального газа, находящегося под воздействием силы гравитационного притяжения (создающей в вертикальном направлении ускорение g = 9,81 м/с2) (рис. 3.6.). К левой и правой стенкам объема О примыкают два тела – 1 и 2 с температурой соответственно Т1 и Т2<Т1. Ясно, что от тела 1 к телу 2 через наш объем начнет передаваться тепловая энергия. Процесс передачи будет сопровождаться круговым движением молекул газа – конвекцией. Качественно этот процесс можно пояснить следующим образом. У левой стенки газ нагревается и расширяется. Его плотность становится меньше, он поднимается вверх и по верхней стенке («потолку») начинает двигаться вправо. Здесь он соприкасается c холодным правым телом, отдает ему часть теплоты и охлаждается. При этом его плотность возрастает, и он начинает опускаться. Холодный газ движется вдоль нижней стенки («пола») влево к горячей стенке. Далее процесс повторяется.
В С
А D
Рис. 3.6. Возникновение упорядоченного движения в идеальном газе
При теплообмене: 1 – источник тепловой энергии; 2 – приемник тепловой энергии (холодильник); 0 – объем идеального газа (открытая система)
Для того чтобы данный процесс рассмотреть количественно, удобно в данном объеме выделить замкнутую трубку движущегося газа.
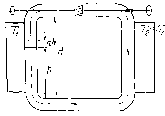
На рисунке 3.7. изображена замкнутая трубка, наполненная газом, с левой стороны которой по-прежнему расположено нагретое тело (источник энергии – 1) с температурой Т1, а с правой – холодное (холодильник –2 – с Т2<Т1). Внутри трубки расположена турбинка, которая преобразует вихревое движение газа по трубке в упорядоченное, вращательное движение.
Газ в левой вертикальной части трубки – АВ – имеет температуру Т1, нагреваясь от источника энергии., а в правой – СД - Т2, отдавая тепло холодильнику.
Распределение давления p1 и плотности молекул газа n1 вдоль высоты h вычисляется следующими соотношениями. Рассмотрим на высоте h объем dV=Пdh (П – площадь поперечного сечения трубки). Число молекул в нем
dN = n1П dh. (3.43,а)
Давление p1, который оказывает газ, находящийся в этом объеме, на его стенки, равно:
p1=КБТ1n1. (3.43,б)
Вес молекул dN равен
dF1= dN·mg=mg n1Пdh, (3.43,в)
где m – масса молекулы газа. Вследствие этого веса давление газа на поперечное сечение трубки, находящееся на высоте h (см. рис. 3.8), меньше, чем на сечение, находящееся на высоте (h+dh) на величину
dp1
= -
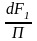=-mgn1dh,
(3.43, г)
Подставляя в (3.43, г) величину n1 из (3.43, б), получаем:
.
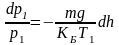(3.43, д)
Интегрируя правую и левую часть выражения (3.43,д) в пределах от 0 до h , получаем
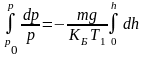или
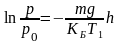(3.43,е)
где p0 – давление газа внизу трубки – на участке DА.
Из (3.43, е) получаем
(3.44)
Аналогично для участка СD получаем
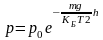(3.44,а)
Если формулах
(3.44) и (3.44,а) заменить Т1
и Т2
произвольной температурой
Т,
а давление p
вычислить по формуле (3.21), то получим
распределение плотности частиц в
зависимости от потенциальной энергии
гравитационного поля
:
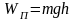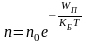(3,45)
где n0 –плотность молекул газа на высоте h=0 (в нашем случае – на участке DA рис. 3.6). Формула (3.45) именуется распределением Больцмана [2, 3]).
Разность давлений между узлами В и С трубки равна
,
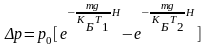(3.46)
где H – высота участков АВ и СD.
Работа, которую совершает газ, чтобы вращать турбину ТРБ (рис. 3.8.), равна
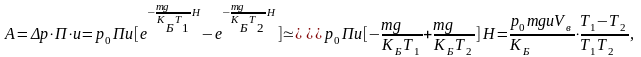(3.47)
где и– средняя скорость движения молекул газа по трубке Vв=SП – объем вертикальных участков трубки АВ и СD.
В трб С
A D