44. Формула Эйлера для шарнирно опертого сжатого стержня

Для шарнирно опертого стержня, сжатого по концам, формула Эйлера для определения критической нагрузки:  (коэффициент приведения длины  ).

Основной случай потери устойчивости – случай, когда при закреплении концов стержня и приложении нагрузки форма потери устойчивости представляет собой одну полуволну синусоиды (рис. 12.2, а).

Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по торцам) легко могут быть приведены к основному случаю потери устойчивости путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.

45. Обобщенная формула Эйлера

Л. Эйлер получил формулу для определения теоретической нагрузки (Эйлерова нагрузка), при которой происходит потеря устойчивости стержня. Формула Эйлера:  , где Е – модуль Юнга;  – минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости);  – коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение  - приведенная длина стержня.

46. Пределы применимости формулы Эйлера. Формула Ясинского. Гипербола Эйлера и прямая Ясинского.

Пределы применимости формулы Эйлера можно установить, предварительно введя понятие гибкости стержня. Определим Эйлеровы напряжения, исходя из формулы Эйлера:

.

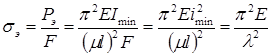Здесь  – минимальный радиус инерции;  –гибкость сжатого стержня:  . Величину в правой части неравенства обозначим   и назовем предельной гибкостью. Тогда  . В отличие от гибкости стержня, предельная гибкость зависит только от физико-механических свойств материала и не зависит от размеров. Предельная гибкость – постоянная для данного материала величина.

Используя понятие предельной гибкости, пределы применимости формулы Эйлера можно представить в виде:  .

Формула Эйлера дает истинное значение нагрузки, при которой происходит потеря устойчивости стержня в случае, когда гибкость рассчитываемого стержня больше или равна предельной гибкости для материала, из которого он изготовлен.

Когда формула Эйлера неприменима (за пределом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.

σ_кр = a – bλ, F_кр = σ_крA ,

здесь a и b коэффициенты, зависящие от материала стержня, измеряются в МПа, приводятся в справочниках.

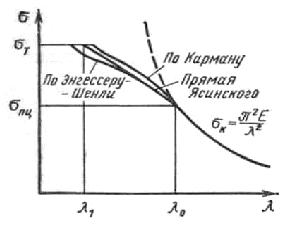Зависимость критических напряжений σ_кр от гибкости λ изображается графически в виде полной диаграммы критических напряжений. На рисунке приведена такая диаграмма для стали

Для стержней малой гибкости зависимость σ_кр от λ выражена горизонтальной прямой , для стержней средней гибкости – наклонной прямой, а для стержней большой гибкости – гиперболой Эйлера. Если известна гибкость рассчитываемого стержня, то критическое напряжение может быть найдено непосредственно по диаграмме критических напряжений.

48. Продольно-поперечный изгиб

Р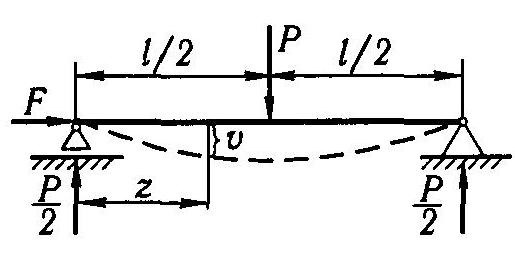 ассмотрим случай одновременного действия на стержень осевой сжимающей силы и поперечной нагрузки (Под действием этой нагрузки стержень деформируется, как показано на рисунке штриховой линией. Если деформации малы по сравнению с размерами сечения, то напряжения в стержне можно определять, пользуясь принципом независимости действия сил, т. е. отдельно от сжимающей силы, по формуле:

и отдельно от поперечной нагрузки, вызывающей изгиб, по формуле:

где Мо — изгибающий момент только от поперечной нагрузки.

Однако с возрастанием гибкости стержня влиянием прогиба на увеличение изгибающего момента от действия продольной силы пренебрегать уже нельзя.

Уравнение для изгибающих моментов

Максимальный изгибающий момент (при z = )

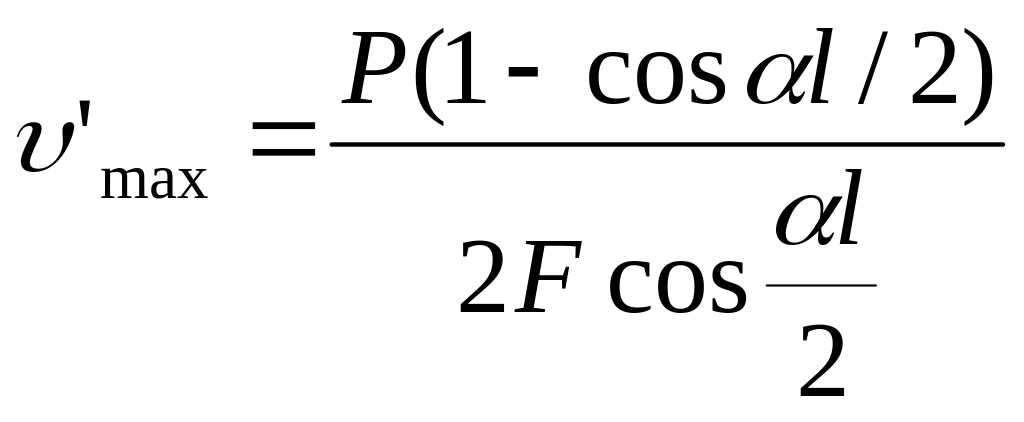. , (при z=0)

значение критической силы, которую иногда называют эйлеровой критической силой.

Это имеет место в том случае, если напряжения в момент потери устойчивости не превосходят предела пропорциональности. При более значительной поперечной нагрузке до потери устойчивости произойдет исчер­пание несущей способности стержня, после того как напряжения в наиболее опасных точках достигнут предела текучести.

При нагрузке, симметричной относительно середины (или близ­кой к симметричной), прогибы определяют по формуле

где — прогиб балки от одной поперечной нагрузки; С — по­правочный коэффициент, равный

(здесь F_cr — критическая сила).