- •24. Определение постоянных при интегрировании дифференциального уравнения изгиба балки.
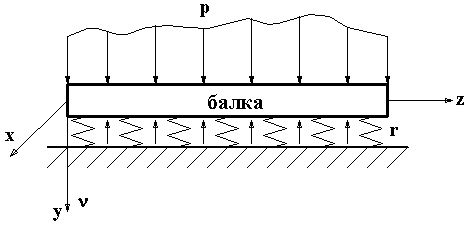
- •27. Балка на упругом основании
- •29. Расчеты бесконечной балки на упругом основании при действии сосредоточенной силы.
- •38. Внецентренное растяжение сжатие (колонны) с учетом собственного веса.
- •41 Кривой брус. Внутренние силовые факторы, их определение и построение эпюр.
- •42. Определение нормальных напряжений при чистом изгибе кривого бруса и положения нулевой линии
- •43. Понятия об устойчивых и неустойчивых формах равновесия систем. Устойчивость сжатых стержней и критическая сила.
- •44. Формула Эйлера для шарнирно опертого сжатого стержня
- •45. Обобщенная формула Эйлера
- •46. Пределы применимости формулы Эйлера. Формула Ясинского. Гипербола Эйлера и прямая Ясинского.
- •48. Продольно-поперечный изгиб
- •49. Динамические нагрузки
- •50. Учет сил инерции. Продольно поперечный удар
24. Определение постоянных при интегрировании дифференциального уравнения изгиба балки.
Дифференциальное уравнение изогнутой оси балки и его интегрирование.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.
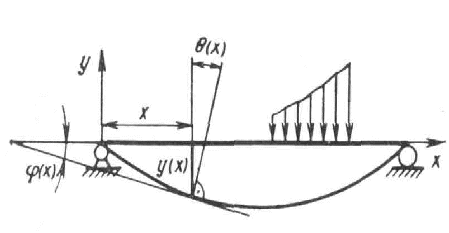
Приближенное дифференциальное
уравнение упругой линии балки
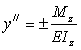
Выбор знака в правой части определяется направлением координатной оси y, так как от этого направления зависит знак второй производной y//. Если ось направлена вверх, то, надо оставить знак плюс. Если же ось направлена вниз, то знаки y// и Mz противоположны - в правой части знак минус. Уравнение справедливо только в пределах применимости закона Гука.
Интегрируя, находим сначала углы поворота сечений
|
|
а после второго интегрирования – прогибы балки
|
|
25. Интегрирование дифференциального уравнения изгиба балки с несколькими участками. Метод Клебша.
Для составления уравнений необходимо выполнить следующие основные условия:
начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z – a), где а – координата сечения, в котором приложен момент;
в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления
Метод начальных параметров
Для углов поворота
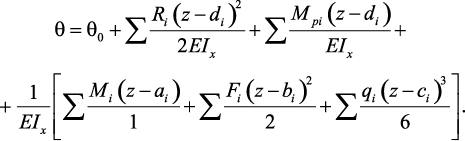 (17)
(17)
Для прогибов:
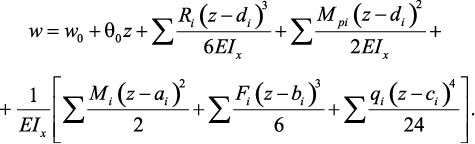 (18)
(18)
где θ – угол поворота сечения; w – прогиб; θo – угол поворота в начале координат; w0 – прогиб в начале координат; dі – расстояние от начало координат до i-й опоры балки; ai – расстояние от начало координат до точки приложения сосредоточенного момента Mi; bi – расстояние от начало координат до точки приложения сосредоточенной силы Fi; сi – расстояние от начало координат до начала участка распределенной нагрузки qi; Ri и Мрi – реакция и реактивный момент в опорах балки.
27. Балка на упругом основании
Рис.10.1 |
В инженерной практике встречаются
балки, лежащие на сплошном упругом
основании. Это ленточные фундаменты
зданий, фундаменты плотин, ж/д шпалы
и др. Расчет таких балок осложняется
тем, что реакция оснований « |
зависит от прогибов «![]() »
балки, а прогибы зависят от реакции
основания. Для решения задачи необходимо
знать закон, связывающий реакцию
основания с осадкой (прогибом) основания.
Наиболее распространенной является
гипотеза Винклера
»
балки, а прогибы зависят от реакции
основания. Для решения задачи необходимо
знать закон, связывающий реакцию
основания с осадкой (прогибом) основания.
Наиболее распространенной является
гипотеза Винклера
![]() (1)
(1)
Обозначим
![]() (2)
(2)
Здесь:
![]() внешняя погонная нагрузка;
внешняя погонная нагрузка;
![]() коэффициент постели, приводится в
справочниках для различных грунтов;
коэффициент постели, приводится в
справочниках для различных грунтов;
![]() суммарная погонная нагрузка, действующая
на балку.
суммарная погонная нагрузка, действующая
на балку.
Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса
![]() (3)
(3)
Обычно
![]() изгибная жесткость балки, считается
константой. Ранее получены дифференциальные
зависимости (1.7)
изгибная жесткость балки, считается
константой. Ранее получены дифференциальные
зависимости (1.7)
![]() (4)
(4)
Дифференцируя один раз (3) с учетом (4) получим
![]() (5)
(5)
Дифференцируя (5) с учетом (4) найдем
![]() (6)
(6)
Подставим (2) в (6)
![]() (7)
(7)
Обозначим
![]()
Тогда уравнение (7) примет вид
![]() (10.1)
(10.1)
Это дифференциальное уравнение балки на упругом основании.
28. Дифференциальное уравнение изгиба балки на упругом основании
Рис.10.1 |
В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется тем, что реакция оснований « » |
зависит от прогибов « » балки, а прогибы зависят от реакции основания. Для решения задачи необходимо знать закон, связывающий реакцию основания с осадкой (прогибом) основания. Наиболее распространенной является гипотеза Винклера
(1)
Обозначим
(2)
Здесь: внешняя погонная нагрузка; коэффициент постели, приводится в справочниках для различных грунтов; суммарная погонная нагрузка, действующая на балку.
Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса
(3)
Обычно изгибная жесткость балки, считается константой. Ранее получены дифференциальные зависимости (1.7)
(4)
Дифференцируя один раз (3) с учетом (4) получим
(5)
Дифференцируя (5) с учетом (4) найдем
(6)
Подставим (2) в (6)
(7)
Обозначим
Тогда уравнение (7) примет вид
(10.1)
Это дифференциальное уравнение балки на упругом основании.