20.Двойной интеграл.Его свойства.Вычисление двойного интеграла в декартовой и полярной системах координат.Геометрическое приложение двойного интеграла.

Двойные интегралы.

Определение: Если при стремлении к нулю шага разбиения области  интегральные суммы имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области .

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

Условия существования двойного интеграла.

Сформулируем достаточные условия существования двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области , то двойной интеграл существует.

Свойства двойного интеграла.

1)

2)

3) Если  = ₁ + ₂, то

4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

5) Если f(x, y)  0 в области , то .

Вычисление двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями х = a, x = b, (a < b), y = (x), y = (x), где  и  - непрерывные функции и

  , тогда

Теорема. Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями y = c, y = d (c < d), x = (y), x = (y) ((y)  (y)), то

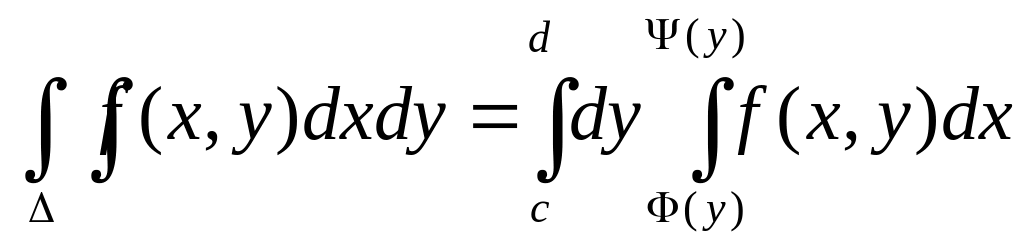
20. Выражение 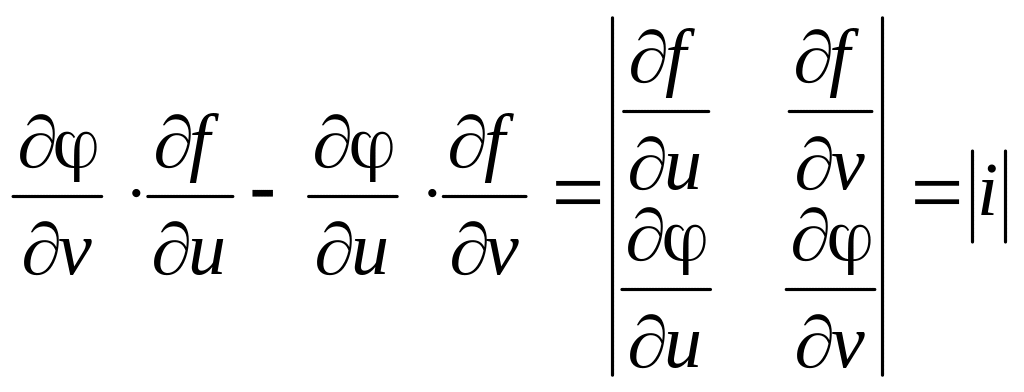называется определителем Якоби или Якобианом функций f(u, v) и (u, v).

Формула замены переменной в двойном интеграле :

Двойной интеграл в полярных координатах.

Воспользуемся формулой замены переменных:

При этом известно, что

В этом случае Якобиан имеет вид:

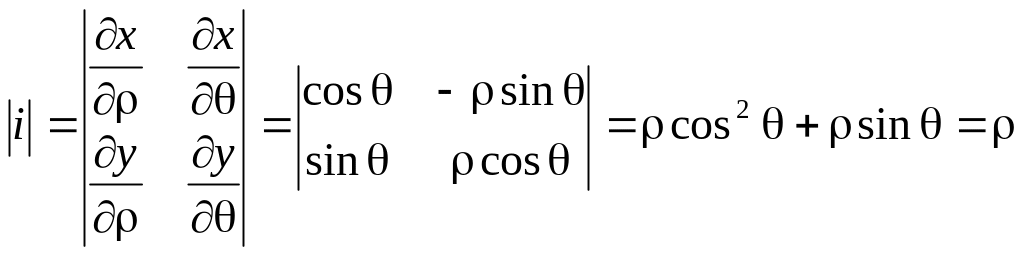
Тогда

Здесь  - новая область значений,

Приложение двойного интеграла:

Вычисление площади .

Вычисление объемов тел. V=

Нахождение массы плоской пластинки m = , где - ф. задающая плотность данной пластинки

21.Тройной интеграл.Его свойства.Вычисление двойного интеграла в декартовой цилиндрической и сферической системах координат.Геометрическое приложение двойного интеграла

Суммирование производится по области v, которая ограничена некоторой поверхностью (x, y, z) = 0.

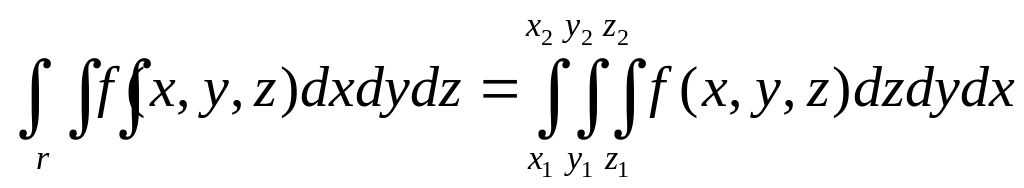
Здесь х₁ и х₂ – постоянные величины, у₁ и у₂ – могут быть некоторыми функциями от х или постоянными величинами, z₁ и z₂ – могут быть функциями от х и у или постоянными величинами.

Замена переменных в тройном интеграле.

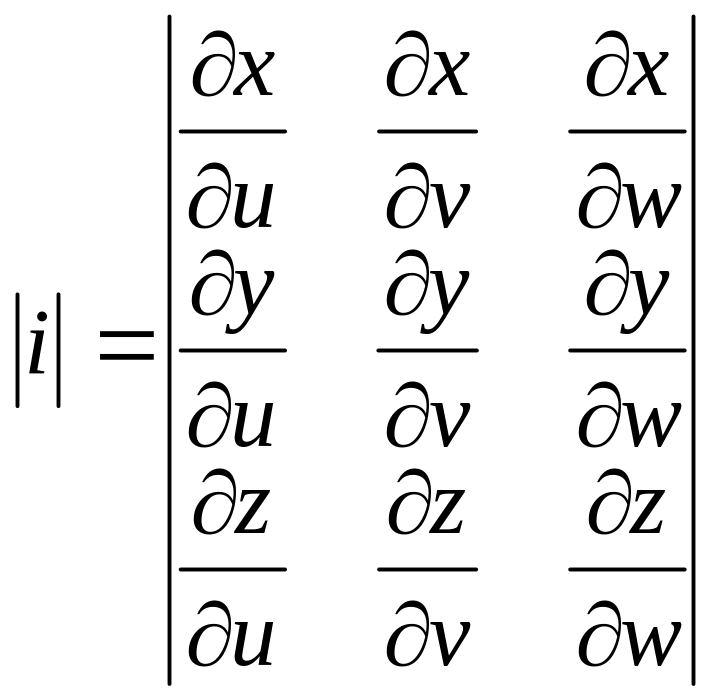
Декартава система :

, Д – проекция области V на плоскость oxy. Если Д явл. Прав. В направлении oy, и огран снизу y=y1(x). Сверху y=y2(x), а по бокам х=а и х=b/

Цилиндрическая система координат.

z

0

 x

y

Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан

_21.

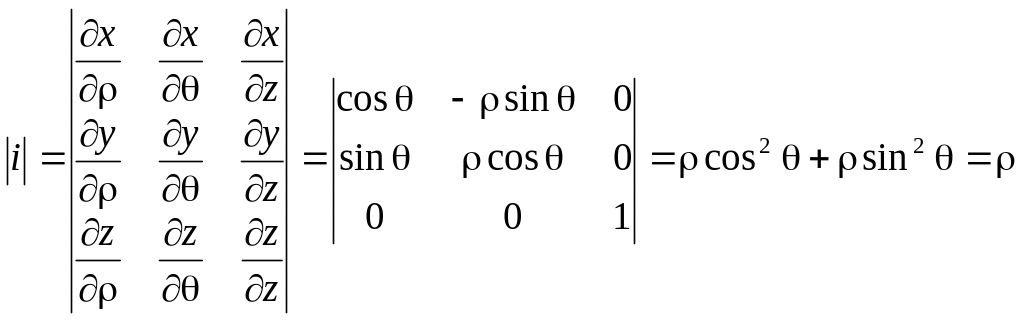
Итого:

Сферическая система координат.

z

P





0  x

y

Геометрическое приложение:

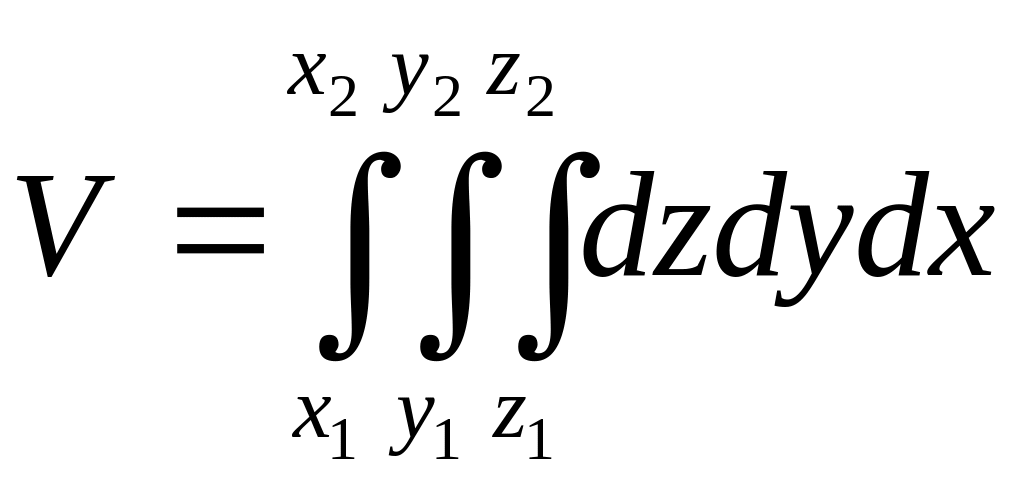
ФОРМУЛЫ

Интеграл		Значение	Интеграл		Значение
1		-lncosx+C	9		ex + C
2		lnsinx+ C	10		sinx + C
3			11		-cosx + C
4			12		tgx + C
5			13		-ctgx + C
6		ln	14		arcsin + C
7			15
8			16