5.4. Структурные диаграммы
|
Основное назначение структурных диаграмм заключается в графическом представлении состава статистических совокупностей, характеризующихся как соотношение различных частей каждой из совокупностей. Состав статистической совокупности графически может быть представлен с помощью как абсолютных, так и относительных показателей. В первом случае не только размеры отдельных частей, но и размер графика в целом' определяются статистическими величинами и изменяются в соответствии с изменениями последних. Во втором - размер всего графика не меняется (так как сумма всех частей любой совокупности составляет 100%), а меняются только размеры отдельных его частей. Графическое изображение состава совокупности по абсолютным и относительным показателям способствует проведению более глубокого анализа и позволяет проводить международные сопоставления и сравнения социально-экономических явлений. В качестве графического образа для изображения структуры совокупностей применяются прямоугольники - для построения столбиковых и полосовых диаграмм и круги - для построения секторных диаграмм. Покажем построение указанных выше диаграмм на конкретных примерах. Чтобы по приведенным данным табл. 5.5 построить диаграмму, отражающую структуру сравниваемых совокупностей по соотношению в них отдельных видов часов, ряд абсолютных показателей заменяется рядом относительных величин. В этом случае каждая из полос диаграммы будет иметь одинаковую длину, так как при переходе к относительным величинам погашаются различия в абсолютных размерах совокупностей. В то же время структурные различия проявляются значительно четче. Графическое изображение структуры с помощью столбиковых (полосовых) диаграмм позволяет изучить особенности многих изучаемых экономических явлений. Так, приведенная на рис. 5.16 диаграмма характеризует увеличение доли наручных часов в общем производстве. Таблица 5.5. Производство часов по видам в одном из регионов России за 1990 - 1998 гг. (цифры условные)
Более распространенным способом графического изображения структуры статистических совокупностей является секторная диаграмма, которая считается основной формой диаграммы такого назначения. Это объясняется тем, что идея целого очень хорошо и наглядно выражается кругом, который представляет всю совокупность. Удельный вес каждой части совокупности в секторной диаграмме характеризуется величиной центрального угла (угол между радиусами круга). Сумма всех углов круга, равная 360°, приравнивается к 100%, а следовательно, 1% принимается равным 3,6°. |
||||||||||||||
11. Линейные алгоритмы.
Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца.
На рис. 11.3 приведен пример блок-схемы алгоритма вычисления периметра Р и площади S квадрата со стороной длины A.
Р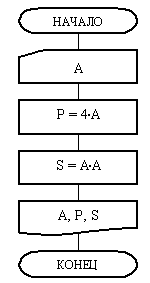
ис.
11.3. Линейный алгоритм
Блок-схема алгоритма состоит из шести блоков. Выполнение алгоритма начинается с блока 1 "Начало". Этот блок символизирует включение автомата, настройку его на выполнение алгоритма и выделение памяти под все переменные, которые задействованы в алгоритме. В алгоритме рис. 11.3 таких переменных три: A, Р, S. Следовательно, под каждую из них алгоритмом будет выделено по одной ячейке памяти. На этом блок 1 будет отработан.
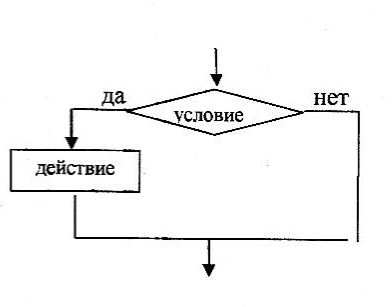
12. Разветвляющиеся алгоритмы. Полная форма ветвления.
13. Разветвляющиеся алгоритмы. Неполная форма ветвления
На практике алгоритмы линейной структуры встречается крайне редко. Чаще необходимо организовать процесс, который в зависимости от каких-либо условий проходит по той либо иной ветви алгоритма. Такой алгоритм называется разветвляющимся.
в неполной форме |
в полной форме
|
I. Содержит только одно действие |
|
1. Алгоритмический язык
|
|
Если условие то действие Всё
|
Если условие то действие 1 иначе действие 2 Всё |
2. Блок-схема |
|
|
|
14 Разветвляющиеся алгоритмы. Выбор.
-
Язык блок-схем
Язык Бейсик
1. если - то
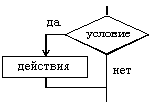
IF условие THEN действия
2. если - то - иначе
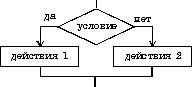
IF условие THEN действие 1 ELSE действие 2
3. выбор
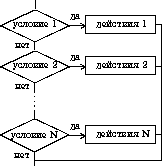
SELECT CASE CASE условие 1 действия 1 CASE условие 2 действия 2 . . . CASE условие N действия N END SELECT
4. выбор - иначе
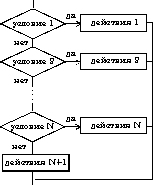
SELECT CASE CASE условие 1 действия 1 CASE условие 2 действия 2 . . . CASE условие N действия N ELSE действия N+1 END SELECT
15.Циклические алгоритмы.
Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма. Различают циклы с заранее известным и заранее неизвестным количеством проходов.
Рассмотрим пример алгоритма с циклом, имеющим заранее неизвестное количество проходов.
Пример 1. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, ..., сумма которых больше числа К.
Блок-схема алгоритма решения этой задачи приведена на рис. 11.5. Она состоит из восьми блоков.
Р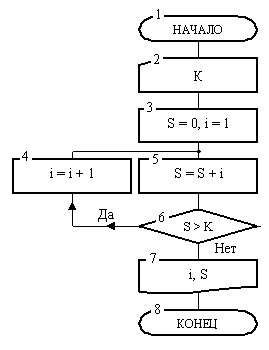
ис.
11.5. Циклический алгоритм с заранее
неизвестным количеством проходов
После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5
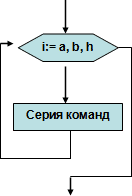
16. Циклические алгоритмы. Оператор цикла с параметром.
Цикл с параметром (иначе цикл для) имеет вид:
Форматы записи операторов алгоритма |
Блок-схема |
Форматы записи операторов на Паскале |
Для i от а до b шаг h делай Нц Серия команд кц |
|
h = +1 for i:= a to b do begin серия команд end; h = -1 for i:= b downto a do begin Cерия команд; end; |
где
i – параметр цикла; a – начальное значение цикла; b – конечное значение цикла; h – шаг изменения параметра.