
- •Обробка масиву даних
- •1. Введення початкових даних і побудова гістограми
- •Xlim([xl xr]); % межі по осі ох
- •2. Вибіркові параметри розподілу (точкові оцінки)
- •3. Довірчі оцінки генеральних параметрів розподілу (інтервальні оцінки)
- •4. Підбір теоретичного розподілу і його параметрів
- •Xlabel('X'), ylabel('f(X)'); % мітки осей
- •Xlim([xl xr]), ylim([0 1.4*max(fv)]); % межі рисунка по осях
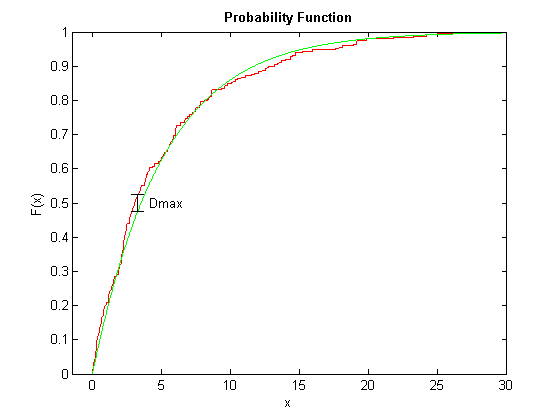
- •5. Критерій узгодженості Колмогорова
- •Xlabel('X'), ylabel('f(X)'); % мітки осей
- •Xlim([xl xr]); % межі по осі ox
- •6. Критерій узгодженості Пірсона
- •7. Додаток
- •If isempty(k)
Xlabel('X'), ylabel('f(X)'); % мітки осей
Xlim([xl xr]); % межі по осі ox
Вибираємо рівень значущості для критерію Колмогорова p=0.30
Найбільш підходящий - показниковий розподіл
Максимальна різниця Dmax=0.06294 досягається при x= 3.88412
Статистика Колмогорова Lambda= 0.99519
Квантиль розподілу Колмогорова Lambda(0.70)= 0.97306
Розподіл підібрано неправильно, так як Lambda>Lambda(1-p)
Якщо у Вашій версії MATLAB немає процедур для обчислення функції, гуснини і квантилів розподілу Колмогорова, можна взяти їх в додатку і записати в будь-який каталог, доступний MATLAB.
6. Критерій узгодженості Пірсона
У критерії
узгодженості Пірсона порівнюються між
собою теоретичні і емпіричні числа
попадань в інтервали. Візьмемо ті
інтервали, по яких була побудована
гістограма. Емпіричні числа попадань
в ці інтервали
![]() ми порівнюємо з теоретичним числом
попадань
ми порівнюємо з теоретичним числом
попадань
![]() ,
де
,
де
![]() – імовірність попадання нашої величини
в
– імовірність попадання нашої величини
в
![]() -й
інтервал. Теоретичний розподіл можна
вважати підібраним вірно на рівні
значущості
,
якщо сумарна квадратична відносна
різниця між теоретичним і практичним
числом попадань в кожен інтервал буде
не дуже великою: повинна виконуватися
умова
-й
інтервал. Теоретичний розподіл можна
вважати підібраним вірно на рівні
значущості
,
якщо сумарна квадратична відносна
різниця між теоретичним і практичним
числом попадань в кожен інтервал буде
не дуже великою: повинна виконуватися
умова
![]() , (0)
, (0)
причому потрібно,
щоб всі
![]() .
.
Побудуємо таблицю
результатів, в яку занесемо: номери
інтервалів (1-й стовпець), межі інтервалів
![]() і
і
![]() (2-й і 3-й стовпці), практичне число попадань
(4-й стовпець), імовірність попадання в
інтервал
(5-й стовпець), теоретичне число попадань
(6-й стовпець) і величини
(2-й і 3-й стовпці), практичне число попадань
(4-й стовпець), імовірність попадання в
інтервал
(5-й стовпець), теоретичне число попадань
(6-й стовпець) і величини
![]() (7-й стовпець).
(7-й стовпець).
Імовірність попадання в -й інтервал обчислюється по формулі
![]() . (0)
. (0)
%% 6. Критерій узгодженості Пірсона
clear Tabl; % очистили таблицю результатів
Tabl(:,1)=[1:k]'; % номери інтервалів
Tabl(:,2)=xm'-delta/2; % ліві межі інтервалів
Tabl(:,3)=xm'+delta/2; % праві межі інтервалів
Tabl(1,2)=-inf; % теоретичний початок 1-го інтервалу
Tabl(k,3)=inf; % теоретичне закінчення останнього інтервалу
Tabl(:,4)=nj'; % дослідні числа попадань
bor=[Tabl(:,2);Tabl(end,3)]; % всі межі інтервалів
pro=[normcdf(bor,mx,sx),expcdf(bor,1/lam),unifcdf(bor,a,b),raylcdf(bor,sig)];
Tabl(:,5)=pro(2:end,nd)-pro(1:end-1,nd);% імовірності попадання pj
Tabl(:,6)=n*Tabl(:,5); % теоретичне число попадань npj
Tabl(:,7)=(Tabl(:,4)-Tabl(:,6)).^2./Tabl(:,6); % відносне квадратичне відхилення
disp('Підсумкова таблиця результатів');
disp(' j aj bj nj pj npj (nj-npj)^2/npj');
fprintf('%2.0f%12.5f%12.5f%6.0f%12.5f%12.5f%12.5f\n',Tabl');
Підсумкова таблиця результатів
j aj bj nj pj npj (nj-npj)^2/npj
1 -Inf 1.99996 66 0.29366 73.41536 0.74899
2 1.99996 3.96831 43 0.20468 51.16884 1.30411
3 3.96831 5.93665 45 0.14537 36.34167 2.06283
4 5.93665 7.90500 29 0.10324 25.81096 0.39402
5 7.90500 9.87335 21 0.07333 18.33173 0.38838
6 9.87335 11.84170 23 0.05208 13.01976 7.65032
7 11.84170 13.81005 7 0.03699 9.24703 0.54603
8 13.81005 15.77840 1 0.02627 6.56752 4.71979
9 15.77840 17.74674 6 0.01866 4.66445 0.38240
10 17.74674 19.71509 2 0.01325 3.31284 0.52026
11 19.71509 21.68344 3 0.00941 2.35288 0.17798
12 21.68344 23.65179 2 0.00668 1.67109 0.06474
13 23.65179 25.62014 0 0.00475 1.18686 1.18686
14 25.62014 27.58849 0 0.00337 0.84294 0.84294
15 27.58849 29.55683 1 0.00239 0.59868 0.26902
16 29.55683 Inf 1 0.00587 1.46738 0.14887
Перевіримо виконання
умови всі
,
і об'єднаємо ті інтервали, в яких
![]() .
Перебудуємо таблицю і підрахуємо
статистику Пірсона. Порівняємо отриману
величину з квантилем
- розподілу Пірсона на заданому рівні
значущості.
.
Перебудуємо таблицю і підрахуємо
статистику Пірсона. Порівняємо отриману
величину з квантилем
- розподілу Пірсона на заданому рівні
значущості.
% Перевірка і усунення інтервалів з попаданнями менше 5
ResTabl=Tabl(1,1:6); % взяли перший рядок
for k1=2:k, % беремо інші рядки таблиці
if ResTabl(end,6)<5, % попередні npj<5 => будемо підсумовувати
ResTabl(end,3)=Tabl(k1,3); % нова права межа інтервалу
ResTabl(end,4:6)=ResTabl(end,4:6)+Tabl(k1,4:6); % підсумовуємо nj, pj, npj
else % попередні npj>=5 => будемо дописувати рядок
ResTabl=[ResTabl;Tabl(k1,1:6)]; % дописуємо рядок
end
end
if ResTabl(end,6)<5, % останнє npj<5
ResTabl(end-1,3)=ResTabl(end,3); % нова права межа інтервалу
ResTabl(end-1,4:6)=ResTabl(end-1,4:6)+ResTabl(end,4:6); % nj, pj, npj
ResTabl=ResTabl(1:end-1,:); % відкинули останній рядок
end
kn=size(ResTabl,1); % число об"єднаних інтервалів
ResTabl(:,1)=[1:kn]'; % нові номери інтервалів
ResTabl(:,7)=(ResTabl(:,4)-ResTabl(:,6)).^2./ResTabl(:,6); % (nj-npj)^2/npj
disp('Згрупована підсумкова таблиця результатів');
disp(' j aj bj nj pj npj (nj-npj)^2/npj');
fprintf('%2.0f%12.5f%12.5f%6.0f%12.5f%12.5f%12.5f\n',ResTabl');
hi2=sum(ResTabl(:,7)); % сума елементів останнього стовпця - статистика Пірсона
fprintf('Статистика Пірсона chi2=%10.5f\n',hi2);
pz=0.1; % вибрали рівень значущості
fprintf('Задаємо рівень значущості p=%5.4f\n',pz);
chi2pz=chi2inv(1-pz,kn-3); % квантиль розподілу Пірсона
fprintf('Квантиль chi2-розподілу Пірсона chi2(%5.2f,%d)=%10.5f\n',1-pz,kn-3, chi2pz);
if hi2<=chi2pz,
disp('Розподіл підібрано правильно, так як chi2<=chi2(1-p,k-3)');
else
disp('Розподіл підібрано неправильно, так как chi2>chi2(1-p,k-3)');
end
Згрупована підсумкова таблиця результатів
j aj bj nj pj npj (nj-npj)^2/npj
1 -Inf 1.99996 66 0.29366 73.41536 0.74899
2 1.99996 3.96831 43 0.20468 51.16884 1.30411
3 3.96831 5.93665 45 0.14537 36.34167 2.06283
4 5.93665 7.90500 29 0.10324 25.81096 0.39402
5 7.90500 9.87335 21 0.07333 18.33173 0.38838
6 9.87335 11.84170 23 0.05208 13.01976 7.65032
7 11.84170 13.81005 7 0.03699 9.24703 0.54603
8 13.81005 15.77840 1 0.02627 6.56752 4.71979
9 15.77840 19.71509 8 0.03191 7.97729 0.00006
10 19.71509 Inf 7 0.03248 8.11983 0.15444
Статистика Пірсона chi2= 17.96896
Задаємо рівень значущості p=0.1000
Квантиль chi2-розподілу Пірсона chi2( 0.90,7)= 12.01704
Розподіл підібрано неправильно, так как chi2>chi2(1-p,k-3)
