Xlabel('X'), ylabel('f(X)'); % мітки осей
Xlim([xl xr]), ylim([0 1.4*max(fv)]); % межі рисунка по осях
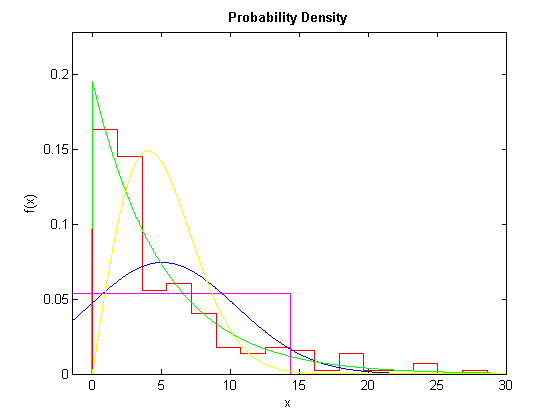
Який теоретичний розподіл найкраще узгоджується з емпіричним: нормальний, показниковий, рівномірний чи Релеєвський?
5. Критерій узгодженості Колмогорова
Критерій узгодженості
Колмогорова застосовується для перевірки
правильності підбору теоретичного
розподілу. Для його застосування потрібно
знайти максимальну по модулю різницю
між теоретичною (генеральною,
передбачуваною, підібраною) функцією
розподілу
і вибірковою (дослідною, емпіричною,
експериментальною)
:
, (0)
а по ній обчислити
,
яку порівняти з квантилем
-розподілу
Колмогорова. Якщо величина
не дуже велика (не перевершує квантиля
),
то на рівні значущості
статистичну гіпотезу можна прийняти.
Якщо ж
то теоретичний розподіл підібраний
неправильно.
Графік емпіричної
функції розподілу
представляє ступінчасту лінію: це ламана
зі сходинками заввишки
в точках з абсцисами
.
Максимум різниці між теоретичною і
емпіричною функціями розподілу
досягається якраз на одній з цих сходинок.
Обчислимо в цих точках
і всі підібрані
,
і для кожної
по формулі (18) знайдемо
.
З цих
виберемо мінімальну – вона відповідатиме
найбільш відповідному виду розподілу.
Побудуємо на одному графіку червоною лінією і найбільш відповідну лінією вибраного раніше кольору. Вертикальною лінією чорного кольору покажемо максимальну по модулю різницю між і . Знайдемо її і обчислимо статистику Колмогорова . Порівняємо знайдену статистику з квантилями - розподілу Колмогорова. Для цього задамо рівень значущості. Зазвичай його вибирають достатньо "жорстким" (тобто великим), наприклад, 0.3.
%% 5. Критерій узгодженості Колмогорова
pk=0.3; % вибрали рівень значущості
fprintf('Вибираємо рівень значущості для критерію Колмогорова p=%4.2f\n',pk);
clear xFv Fv xFt Ft; % очищаемо масиви для функцій розподілу
xFv=[x';x']; % аргументи для побудови вибіркової F(x): 2 стрічки
xFv=[xl;reshape(xFv,2*n,1);xr]; % перетворили в стовпець і додали крайні
Fv=[0:1/n:1]; % значення вибіркової функції розподілу - 1 рядок
Fv=[Fv;Fv]; % 2 рядки для побудови вертикальних сходинок
Fv=reshape(Fv,prod(size(Fv)),1); % порахували вибіркову F(x) – 1 стовпець
Ft=[normcdf(xFv,mx,sx),expcdf(xFv,1/lam),unifcdf(xFv,a,b),raylcdf(xFv,sig)];
[D,imax]=max(abs([Fv,Fv,Fv,Fv]-Ft)); % найшли максимальні різниці
[Dmax,nd]=min(D); % найменша D и номер найбільш підходящого розподілу
im=imax(nd); xDmax=xFv(im); % номер точки і x, де досягається Dmax
fprintf('Найбільш підходящий - %s\n',s{nd});
fprintf('Максимальна різниця Dmax=%7.5f досягається при x=%8.5f\n',Dmax,xDmax);
Xv=[xDmax-d/4,xDmax+d/4,xDmax,xDmax,xDmax-d/4,xDmax+d/4]; % для малювання лінії
Yv=[Fv(im),Fv(im),Fv(im),Ft(im,nd),Ft(im,nd),Ft(im,nd)];
Lambda=Dmax*n^0.5; % статистика
Lam1p=kolminv(1-pk); % і квантиль розподілу Колмогорова
fprintf('Статистика Колмогорова Lambda=%8.5f\n',Lambda);
fprintf('Квантиль розподілу Колмогорова Lambda(%4.2f)=%8.5f\n',1-pk,Lam1p);
if Lambda<=Lam1p,
disp('Розподіл підібрано правильно, так як Lambda<=Lambda(1-p)');
else
disp('Розподіл підібрано неправильно, так як Lambda>Lambda(1-p)');
end
xFt=linspace(xl,xr,1000)'; % абсциси для теоретичної F(x)
Ft=[normcdf(xFt,mx,sx),expcdf(xFt,1/lam),unifcdf(xFt,a,b),raylcdf(xFt,sig)];
f3=figure;
plot(xFv,Fv,'-r', xFt,Ft(:,nd),col(nd),Xv,Yv,'-k') % малюємо
text(xDmax+d/2,mean(Yv),'Dmax'); % підписуємо Dmax
title('\bfProbability Function'); % заголовок