Обробка масиву даних

1. Введення початкових даних і побудова гістограми

Почнемо обробку масиву даних з їх введення. У прикладі дані згенеровано генератором випадкових чисел, а також передбачено їх введення з файлу. Позначимо дані змінною . Відсортуємо дані, знайдемо мінімальне і максимальне значення. Знайдемо кількість даних і число степенів свободи вибірки .

% Згенерований розподіл

lambda=5;

tmp=250;

x=exprnd(lambda, tmp, 1); % Згенерувати випадкову послідовність

% або можна завантажити цю послідовність з файлу

%x=load('C:\Matlab\data.txt'); % ПОСТАВТЕ ТУТ СВІЙ КАТАЛОГ І ІМ'Я ФАЙЛУ

x=sort(x); % сортуємо дані у порядку зростання

n=length(x); % довжина даних

f=n-1; % кількість степенів свободи вибірки

xmin=min(x); % мінімальне значення

xmax=max(x); % максимальне значення

fprintf('Об"єм вибірки n=%d\nЧисло степенів свободи f=n-1=%d\n',n,f);

fprintf('xmin=%14.7f xmax=%14.7f\n',xmin,xmax);

Об"єм вибірки n=250

Число степенів свободи f=n-1=249

xmin= 0.0316100 xmax= 31.5251823

Для побудови гістограми інтервал зміни даних потрібно розбити на ділянки однакової довжини. З одного боку, число таких ділянок повинне бути якомога більше, а з іншого, в кожну з цих ділянок повинно потрапляти якомога більше значень . Компроміс між цими вимогами приводить до того, що зазвичай вибирають число інтервалів для побудови гістограми як найближче ціле до . Визначимо ширину кожного інтервалу . 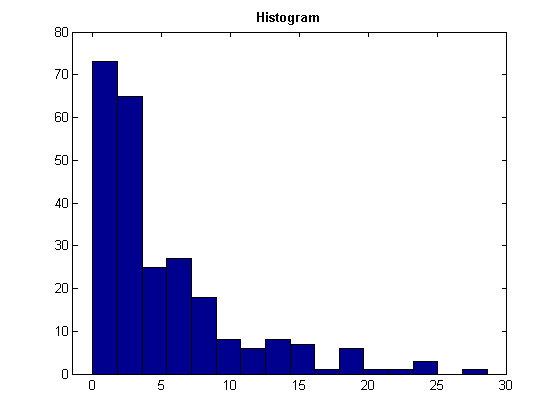Побудуємо гістограму розподілу.

%% 1.2 Побудова гістограми

k=round(n^0.5); % кількість інтервалів гістограми

d=(xmax-xmin)/k; % ширина інтервалу

del=(xmax-xmin)/20; % + малі інтервали спочатку і вкінці для наглядності

xl=xmin-del; xr=xmax+del; % границі інтервалів для побудови графіка

fprintf('Число інтервалів k=%d\nШирина інтервалу h=%14.7f\n',k,d);

f1=figure;

hist(x,k); % побудова гістограми

title('\bfHistogram'); % заголовок

Xlim([xl xr]); % межі по осі ох

Число інтервалів k=16

Ширина інтервалу h= 1.9683483

2. Вибіркові параметри розподілу (точкові оцінки)

Для вибірки визначимо вибіркові математичне очікування , дисперсію , середньоквадратичне відхилення , асиметрію і ексцес , а також коефіцієнт варіації по формулах:

, (0)

, (0)

, (0)

, (0)

. (0)

(5.1)

%% 2. Вибіркові параметри розподілу (точкові оцінки)

Mx=mean(x); % математичне очікування м.о.

Sx=std(x); % середньоквадратичне відхилення с.к.в.

Dx=Sx^2; % дисперсія

Ax=sum((x-Mx).^3)/(n-1)/Sx^3; % коефіцієнт асиметрії

Ex=sum((x-Mx).^4)/(n-1)/Dx^2-3; % коефіцієнт ексцесу

Vx=Sx/Mx; % коефіцієнт варіації

disp('Вибіркові параметри розподілу:');

fprintf('Математичне очікування Mx=%14.7f\n',Mx);

fprintf('Середньоквадратичне відхилення Sx=%14.7f\n',Sx);

fprintf('Дисперсія Dx=%14.7f\n',Dx);

fprintf('Асиметрія Ax=%14.7f\nЕксцес Ex=%14.7f\n',Ax,Ex);

fprintf('Варіація Vx=%14.7f\n',Vx);

Вибіркові параметри розподілу:

Математичне очікування Mx= 5.7526168

Середньоквадратичне відхилення Sx= 5.2622756

Дисперсія Dx= 27.6915447

Асиметрія Ax= 1.6844558

Ексцес Ex= 3.9463752

Варіація Vx= 0.9147621