Численное решение дифференциальных уравнений Основные определения и постановка задачи

Дифференциальное уравнение 1-го порядка, разрешенное относительно производной, имеет вид: (1)

Решением дифференциального уравнения (1) называется функция y(x), подстановка которой в уравнение обращает его в тождество: .

График решения y=y(x) называется интегральной кривой.

Задача Коши для дифференциального уравнения (1) состоит в том, чтобы найти решение дифференциального уравнения (1), удовлетворяющее начальному условию y(x₀)=y₀ (2). Пару чисел (x₀,y₀) называют начальными данными.

Решение задачи Коши называется частным решением дифференциального уравнения (1) при условии (2).

Геометрически задача Коши означает, что требуется найти интегральную кривую y=y(x), проходящую через заданную точку (x₀,y₀).

Теорема о существовании и единственности решения задачи Коши.

Пусть функция f(x,y) – правая часть уравнения - непрерывна вместе со своей частной производной по переменной y в некоторой области D на плоскости. Тогда при любых начальных данных (x₀,y₀)D задача Коши имеет единственное решение y=y(x).

При выполнении условий теоремы через точку (x₀,y₀) на плоскости проходит единственная интегральная кривая.

В классическом анализе разработано немало приемов решения дифференциальных уравнений, однако при решении практических задач эти методы не дают результата. В этом случае прибегают к методам приближенного решения дифференциальных уравнений. В зависимости от формы представления решения выделяют

• аналитические методы (решение в виде аналитического выражения);

• графические методы (решение в виде графика);

• численные методы (решение в виде таблицы).

Численное решение задачи Коши состоит в том, чтобы получить искомое решение y(x) в виде таблицы его приближенных значений аргумента x на некотором отрезке [a, b]:

x₀=a, x₁, x₂, …, x_m=b (3)

Точки (3) называют узловыми, множество этих точек называют сеткой на отрезке [a, b].

Как правило, используют равномерную сетку с шагом h:

x_i=x₀+ih (i=0, 1, …, m)

Приближенные значения численного решения задачи Коши в узловых точках обозначим y_i. y_i  y(x_i), где (i=0, 1, …, m)

Начальное условие выполняется точно: y₀ = y(x₀).

Величина погрешности численного решения задачи Коши на сетке отрезка [a, b] оценивается величиной ,

т.е. расстоянием между векторами приближенного решения (y₀, y₁, …,y_m) и точного решения (y(x₀), y(x₁), …,y(x_m)) на сетке по m-норме.

Метод Эйлера

В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера.

Угловой коэффициент касательной к интегральной кривой в точке M₀(x₀,y₀) равен .

Найдем ординату y₁ касательной, соответствующей абсциссе x₁=x₀+h.

Уравнение касательной к кривой в точке M₀ имеет вид или , откуда y₁=y₀+hf(x₀,y₀).

Аналогично, угловой коэффициент касательной к интегральной кривой в точке M₁(x₁,y₁) равен . Точку M₂(x₂,y₂) получим соответственно

x₂=x₁+h y₂=y₁+hf(x₁,y₁).

Продолжая вычисления по данной схеме, получим формулы Эйлера для приближенного решения задачи Коши с начальными данными (x₀,y₀) на сетке отрезка [a, b] с шагом h:

x_i=x_i-1+h y_i=y_i-1+hf(x_i-1,y_i-1). (4)

Г

M₄

M₃

рафической иллюстрацией приближенного решения является ломаная, соединяющая последовательно точки M₀, M₁, …,M_m, которую называют ломаной Эйлера.

M₂

y

M₁

M₀

x

x₀ x₁ x₂ x₃ x₄

O

Погрешность метода Эйлера можно оценить неравенством

, (5)

которое можно представить в виде d=Ch, где . Таким образом, метод Эйлера имеет первый порядок точности.

Практическую оценку погрешности решения, найденного на сетке с шагом h/2, в точке x_i[a, b] производят с помощью приближенного равенства – правила Рунге:

(6)

где P – порядок точности численного метода.

Таким образом, оценка полученного результата по правилу Рунге вынуждает проводить вычисления дважды: с шагом h и h/2, причем совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

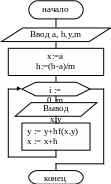
Блок-схема решения ДУ методом Эйлера

Программа решения дифференциального уравнения методом Эйлера

program Eiler;

var x,a,b,h,y:real;

m,i:integer;

function f(x,y: real): real;

begin f:=cos(x);

end;

begin writeln('Введите значения концов отрезка [a,b]');

readln(a,b);

writeln('Введите начальное значение y0=y(x0)');readln(y);

writeln('Введите число значений функции на промежутке [a,b]'); read(m);

x:=a; h:=(b-a)/m;

for i:=0 to m do

begin writeln (x:10:3, y:15:4);

y:=y+h*f(x,y); x:=x+h

end; readln;

end.