Тема 3. Модели задач линейного программирования

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию (линейную форму), оптимум которой требуется найти по условию; ограничения в виде линейных уравнений (неравенств); требования неотрицательности переменных.

В общем виде эта модель сводится к следующему.

Найти оптимум (максимум или минимум) функции

Q(x)= p₁ x₁ + p₂ x₂. . . + p_nx_n

при выполнении ограничений:

a ₁₁ x₁ + a₁₂ x₂. . . + a_1nx_n = b₁

a₂₁ x₁ + a₂₂ x₂. . . + a_2nx_n = b₂

...

a_m1 x₁ + a_m2 x₂. . . + a_mnx_n = b_m

x₁ >= 0, x₂ >=0, ... ,x_n >=0

Задача 3. Небольшое предприятие выпускает два типа автомобильных деталей. Оно закупает литье, подвергаемое токарной обработке, сверловке и шлифовке. Данные, характеризующие производительность станочного парка, приведены в таблице.

Станки	Производительность станочного парка
	Деталь А, штук/час	Деталь Б, штук/час
Токарные	25	40
Сверлильные	28	35
Шлифовальные	35	25

Каждая отливка, из которой изготовляют деталь А, стоит $2. Стоимость отливки для детали Б -$3. Продажная цена деталей равна соответственно $5 и $6. Стоимость часа станочного времени составляет по трем типам используемых станков соответственно $20, $14, $17.5.

Предполагая, что можно выпускать для продажи любую комбинацию деталей А и Б, нужно найти план выпуска продукции, максимизирующий прибыль.

Методические указания к решению

Первый шаг решения заключается в расчете прибыли на деталь. Этот расчет приведен в таблице:

Операции	Деталь А	Деталь Б
Токарная обработка	20/25=0.8	20/40=0.5
Сверление	14/28=0.5	14/35=0.4
Шлифование	17.5/0.5	17.5/25=0.7
Покупная цена	2.00	3.00
Общие затраты	3.8	4.6
Продажная цена	5.0	6.0
Прибыль	1.2	1.4

Если в среднем выпускать в час x деталей А и y деталей Б, то чистая прибыль за это время составит Z=1.2*x+1.4*y.

Поскольку отрицательные значения x и y не имеют смысла, должны удовлетворяться ограничения: x>=0, y>=0.

Кроме того, должны удовлетворяться неравенства:

токарная обработка x/25+y/40<=1

сверление x/28+y/35<=1

шлифование x/35+y/25<=1

Избавляясь от знаменателей, получаем:

токарная обработка 40x+25y<=1000

сверление 35x+28y<=980

шлифование 25x+35y<=875

Таким образом, имеется задача линейного программирования:

Z=1.2*x+1.4*y  max

4 0x+25y<=1000

35x+28y<=980

25x+35y<=875

x>=0, y>=0,

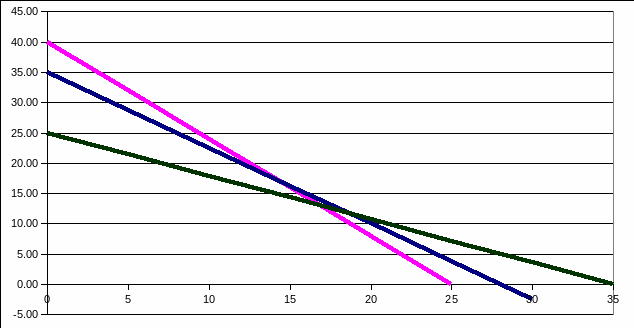
решение которой можно найти графически (рис.2) , поскольку в задаче две переменные.

2

x

y

Рис. 2. Графическое решение задачи линейного программирования

Ограничения по сверлению являются избыточными, поскольку линия 35x+28y<=980 лежит вне пределов области допустимых решений, заштрихованную на рисунке.

Решение задачи следует искать в угловых точках (0,0), (0,25), (25,0) и точке пересечения прямых 40x+25y<=1000 и 25x+35y<=875. Это точка с координатами x=16.9, y=12.9. Но поскольку количество деталей - целое число, следует округлить результаты с недостатком (иначе будет недостаточно ресурсов). Решением задачи можно считать следующий план: число деталей А=16, число деталей В = 12. При этом прибыль предприятия составит 1.2*16+1.4*12 =36.