Решение.

Под знаком предела имеет место неопределенность вида . Воспользуемся правилом Лопиталя.

= =  = .

Если  ≤ 1, то предел равен 0. При   > 1 получаем неопределенность вида , поэтому применим правило Лопиталя еще раз.

 = = .

При α ≤ 2 предел равен 0, если α > 2 опять получаем неопределенность . Пусть k  наименьшее натуральное число большее α. Применив правило Лопиталя k раз, получим

 = = 0.

2. Другие типы неопределенностей

Кроме изученных выше неопределенностей видов и часто встречаются неопределенности следующих видов: 0  ,   , 1^, 0⁰, ⁰. Все эти неопределенности сводятся к двум, изученным выше, путем алгебраических преобразований.

1. Раскрытие неопределенностей вида (0 · ∞). Рассмотрим функции f (x) и g (x). Пусть f (x) = 0, g (x) = ∞, тогда произведение этих функций всегда можно представить в виде

f (x)·g (x) = = ,

то есть при х  а выражение представляет собой неопределенность вида , а выражение  неопределенность вида .

Пример 4. Найти предел ln x.

Решение.

Выражение, стоящее под знаком предела, представляет неопределенность 0 · ∞. Представим это выражение в виде и найдем предел по правилу Лопиталя.

ln x = = 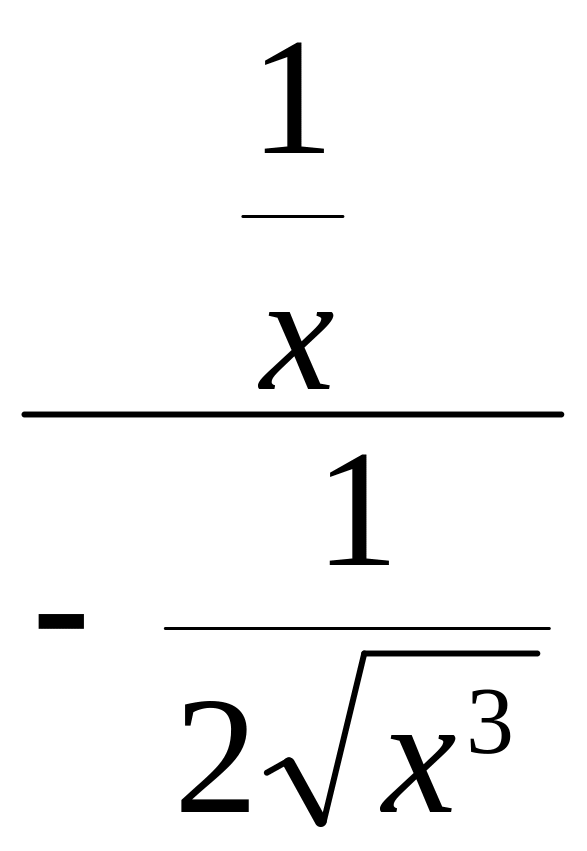= 2 = 2 = 0.

2. Раскрытие неопределенностей вида 1^, 0⁰, ⁰. Каждая из этих неопределенностей имеет вид y = . Прологарифмируем данное выражение (считаем, что f (x) > 0). Получим ln y = g (x)  ln (f(x)). В любом из трех случаев выражение g (x)  ln (f(x)) представляет собой при х  а неопределенность вида 0  , которая рассматривалась выше.

Пример 5. Найти (ctg х) ^sin x.

Решение.

Пусть у =  (ctg х) ^sin x, тогда ln y = sin x  ln (ctg х)  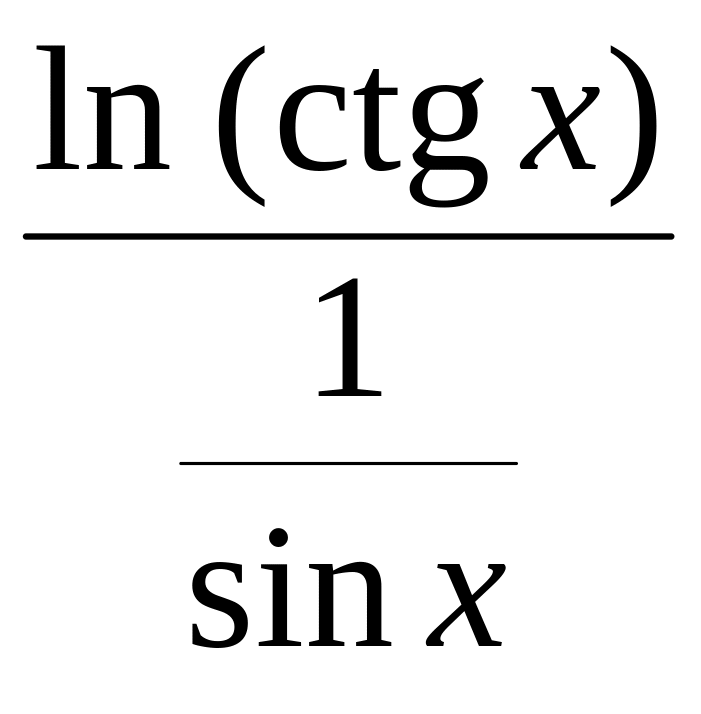= . Применяя правило Лопиталя, будем иметь

 =   =   =  = 0.

Отсюда у = e⁰ = 1.

§ 1.3. Формула тейлора

1. Формула Тейлора для многочлена

Формула Тейлора является одной из основных формул математического анализа и имеет многочисленные применения.

Рассмотрим сначала формулу Тейлора для многочлена.

Рассмотрим многочлен степени n

P(x) = b₀ + b₁x + … + b_nxⁿ. (1)

Выберем произвольным образом точку a, и сделаем подстановку x = (x –  a) + a. Получим

P(x) = b₀ + b₁((x – a) + a) + … + b_n ((x  a) + a)ⁿ =

= β₀ + β₁(x – a) + … + β_n (x - a)ⁿ = β_k(x – a) ^k , (2)

где β_i  некоторые постоянные.

Равенство (2) называется разложением многочлена P(х) по степеням x  a, а числа β_i называются коэффициентами этого разложения.

Найдем коэффициенты β_i, предполагая, что известны значения P (a), P´(a), … , P⁽ⁿ⁾(a). Для этого найдем производные многочлена P(x) до n-ого порядка включительно, и значения этих производных в точке a. Получим

P(a) = β₀, P´(a) = β₁, P´´(a) = 2! β₂, P´´´(a ) = 3! β₃, …, P⁽ⁿ⁾(a) = n! β_n..

Следовательно, β₀ = P(a), β₁ = , β₂ = , …, β_n = . Значит многочлен можно записать в виде

P(x) = P(а) + (x  а) + (x  а)² + …+ (x  а)ⁿ =

= (x  а)^k. (3)

Формула (3) носит название формулы Тейлора для многочлена P(x).

Формула Тейлора для разложения многочлена P(x) по степеням x (при a = 0) имеет вид

P(x) = P(0) + x + …+ xⁿ = x^k. (4)

и называется формулой Маклорена.

Пример. Разложить по формуле Маклорена многочлен P(x) = (x + a)ⁿ.