
- •§ 1.1. Основные теоремы
- •2. Теорема Ролля
- •3. Теорема Лагранжа
- •4. Теорема Коши
- •§ 1.2. Правило лопиталя
- •1. Раскрытие неопределенностей вида и
- •Решение.
- •Решение.
- •Решение.
- •2. Другие типы неопределенностей
- •Решение.
- •Решение.
- •§ 1.3. Формула тейлора
- •1. Формула Тейлора для многочлена
- •Решение:
- •2. Формула Тейлора для произвольной функции
- •4. Разложение элементарных функций по формуле Маклорена
- •5. Примеры применения формулы Маклорена
- •2. Нахождение пределов.
- •§ 1.4. Исследование функции
- •Решение.
- •2. Точки экстремума функции. Необходимое и достаточное условия экстремума функции
- •Р ешение.
- •Решение.
- •Решение.
- •3. Асимптоты графика функции
- •5. Схема полного исследования функции
- •Решение.
- •6. Наибольшее и наименьшее значение функции
- •Решение.
- •Решение.
- •II. Неопределенный интеграл
- •§ 2.1. Первообразная и неопределенный интеграл
- •1. Понятие первообразной и неопределённого интеграла
- •2. Основные свойства неопределённого интеграла
- •3. Таблица основных неопределенных интегралов
- •Решение.
- •4. Интегрирование заменой переменной (метод подстановки)
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •4. Интегрирование по частям
- •Решение.
- •Решение.
- •§ 2.2. Интегрирование рациональных дробей
- •1. Разложение рациональной дроби на сумму простейших дробей
- •Решение.
- •Решение.
- •2. Интегрирование простейших рациональных дробей
- •Решение.
- •Решение.
- •§ 2.3. Интегрирование некоторых тригонометрических и иррациональных выражений
- •1. Интегрирование тригонометрических выражений
- •Решение.
- •Решение.
- •2. Интегрирование иррациональных выражений вида
- •Решение.
- •Решение.
- •3. Интегрирование биноминальных дифференциалов
- •Решение.
- •4. Интегрирование выражений содержащих квадратный трехчлен под знаком корня
- •Решение.
- •Решение.
- •III. Определенный и несобственный интегралы
- •§ 3.1. Понятие определенного интеграла
- •1. Задача о нахождении площади криволинейной трапеции
- •2. Интегральные суммы. Понятие определенного интеграла
- •3. Суммы Дарбу
- •4. Условие существования определенного интеграла
- •5. Классы интегрируемых функций
- •§ 3.2. Свойства определенного интеграла
- •1. Свойства, выраженные равенствами
- •2. Свойства, выраженные неравенствами
- •3. Теоремы о среднем
- •§ 3.3. Нахождение определенных интегралов
- •1. Интегралы с переменным верхним пределом
- •2. Формула Ньютона–Лейбница
- •Решение.
- •3. Формула замены переменной в определенном интеграле
- •Решение.
- •4. Формула интегрирования по частям в определенном интеграле
- •Решение.
- •§ 3.4. Несобственные интегралы
- •1. Несобственный интеграл первого рода
- •Решение.
- •Решение.
- •2. Несобственный интеграл второго рода
- •Решение.
- •IV. Геометрические и физические приложения определенного интеграла
- •§ 4.1. Длина дуги кривой
- •1. Понятие длины дуги кривой
- •2. Нахождение длины дуги кривой
- •Решение.
- •3. Случай пространственной кривой
- •§ 4.2. Площадь плоской фигуры
- •1. Понятие площади фигуры
- •2. Площадь криволинейной трапеции
- •3. Площадь криволинейного сектора
- •§ 4.3. Объем тел
- •2. Нахождение объемов тел
- •3. Площадь поверхности вращения
- •Решение.
- •§ 4.4. Некоторые физические приложения определеннго интеграла
- •1. Масса и центр тяжести
- •Список литературы
- •Ж.В. Иванова т.Л. Сурин с.В. Шерегов
3. Таблица основных неопределенных интегралов
Из формулы (2) и таблицы производных основных элементарных функций получим следующую таблицу основных неопределенных интегралов.
0 dx = C.
1 dx = х + C.
xdx = + C ( ≠ -1).
= ln | x | + C (х 0).
cos x dx = sin x + C.
sin x dx = cos x + C.
 =
tg
x + C ( х
=
tg
x + C ( х
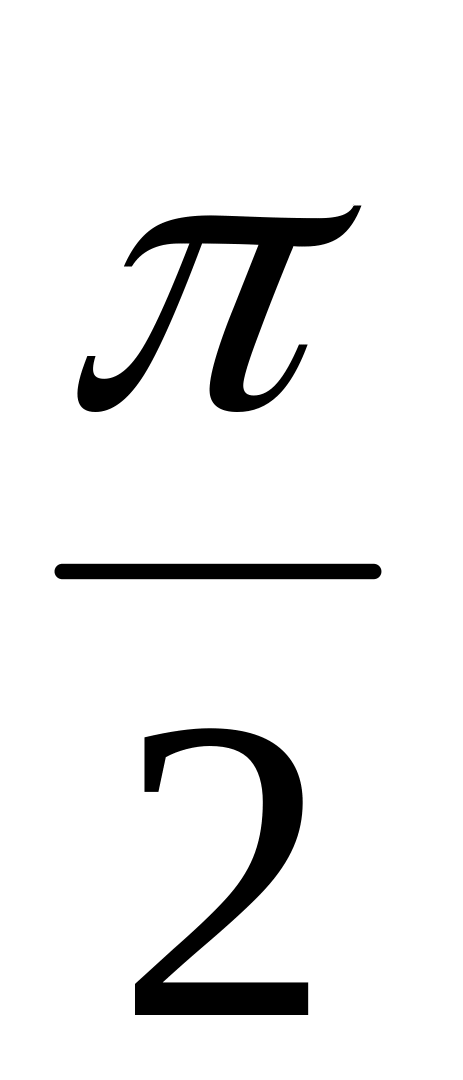 + n,
n
Z).
+ n,
n
Z).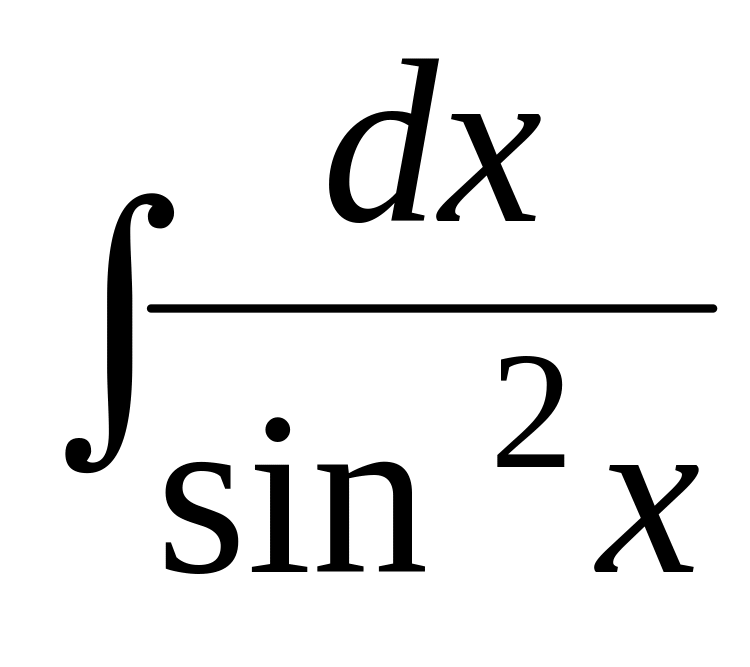 =
ctg
x + C ( х
n,
n
Z).
=
ctg
x + C ( х
n,
n
Z).aх dx = + C,
в частности, eх dx = eх + C.
= arctg x + C,
или более общий случай: = arctg + C.
= (1 < x < 1).
или = (a < x < a).
= ln | x + | + C, > 0
(в
случае знака «»,
|x| > ![]() ).
).
= ln + C ( x a).
К этим формулам можно присоединить и соответствующие формулы для гиперболических функций.
ch x dx = sh x + C.
sh x dx = ch x + C.
 =
th
x + C.
=
th
x + C. =
cth
x + C (x 0).
=
cth
x + C (x 0).
Замечание 1. Формул, аналогичных формулам 12 и 13, в таблице производных нет, но они легко доказываются. Для этого достаточно убедиться, что производные выражений, стоящих в правых частях этих равенств равны подынтегральным функциям.
Пример 1. Используя свойства и таблицу неопределенных интегралов, найти следующие интегралы:
a) (4x3 + + 3(x+1)2)dx;
б) cos 2 dx.
Решение.
а) Используя свойства 3 и 4, а также формулы 2 и 3 из таблицы интегралов, найдем интеграл
(4x+
+ 3(x+1)) dx
= 4
xdx
+ 2
х![]() dx
+ 3
(x2
+ 2х
+ 1)
dx =
dx
+ 3
(x2
+ 2х
+ 1)
dx =
= 4 xdx + 2 х dx + 3 x2 dx + 6 х dx + 3 dx =
=
4![]() + 2(2)
+ 2(2)![]() + 3
+ 3![]() + 6
+ 6
![]() + 3х
+ С =
х4
+ 3х
+ С =
х4
![]() + х3
+ 3х2
+ 3х
+ С.
+ х3
+ 3х2
+ 3х
+ С.
б) Воспользуемся формулой cos = , которая называется формулой понижения степени, и применим свойства 3 и 4 неопределенных интегралов, тогда
cos
dx
=
dx
=
![]() (
cos
x dx +
dx)
=
(
cos
x dx +
dx)
=
=
(
sin
x + х) + С
=
![]() + С.
+ С.
Замечание 2. Производная любой элементарной функции является элементарной функцией. Однако интегралы от некоторых элементарных функций не являются элементарными функциями. Например, приведенные ниже интегралы являются неэлементарными функциями:
1.
![]() dx;
4.
dx;
4.
![]() ;
;
2.
![]() dx; 5.
dx; 5.
![]() ;
;
3.
![]() dx; 6.
dx; 6.
![]() .
.
Каждый из указанных интегралов есть функция не являющаяся элементарной. Эти функции наряду с элементарными широко используются в различных разделах физики, теории вероятностей, статистике.
4. Интегрирование заменой переменной (метод подстановки)
Метод замены переменной один из основных методов нахождения неопределенных интегралов.
Теорема 2. Пусть функция t = (x) определена и дифференцируема на интервале X и множеством значений этой функции является интервал T. Пусть y = f (t) определена на интервале T, тогда, если для f (t) на этом интервале существует первообразная F (t), то функция F ( (x)) является первообразной для функции f ( (x)) '(x) на интервале X и выполняется равенство
f ( (x)) ´(x) dx = F ( (x)) + C. (3)
Доказательство.
Найдём производную функции F ( (x)), по правилу дифференцирования сложной функции
F( (x))' = F '(t) '(x) = f(t)(x) = f ( (x)) '(x),
следовательно, функция F ( (x)) является одной из первообразных функции f ( (x)) '(x) на интервале X и выполняется равенство (3).
Замечание 1. На практике метод замены переменной используется следующим образом: пусть (x) = t, значит ´(x) dx = d( (x)) = dt. Тогда
f ((x)) ´(x) dx = f (t) dt = F (t) + C = F ( (x)) + C.
Нахождение интегралов с помощью формулы (3) называется методом подстановки или интегрированием с помощью замены переменной.
Пример 1. Найти интеграл sin x cos x dx.
