2. Структурная схема программного обеспечения

1. Варианты реализации

Были рассмотрены несколько вариантов реализации: MS Excel, язык программирования С, MathLab.

Реализация в MS Excel

Достоинства

• легкое наглядное представление результата;

• относительно низкая стоимость.

Недостатки

• относительно низкая скорость вычисления;

• невозможность переноса программы куда-либо.

Реализация на языке С

Достоинства:

• возможность относительно легкого переноса программного кода для выполнения на контроллере без участия ПК;

• С – компилируемый язык, соответственно быстрее исполняется программа;

• возможность написания программы без использования больших библиотек;

• наличие бесплатного компилятора.

Недостатки

• сложность реализации программы и наглядного представления результатов работы;

• скорость разработки.

Реализация в MathLab

Достоинства

• легкость разработки и представления результата;

• возможность «выгрузки» программного кода, ориентированного на конкретную систему.

Недостатки

• большая стоимость.

В предлагаемой ВКР выбран вариант реализации на языке C, как язык, наиболее близкий к машинному уровню, обеспечивающий быстрое выполнение программного кода и не требующий затрат на покупку компилятора.

4. Задачи статистической обработки изометрических данных

В конечном итоге целью разработки анализатора является автономный прибор на базе микроконтроллера, что налагает ограничения на используемые алгоритмы и методы их реализации. Например, нецелесообразно подключать библиотеку математических функций из-за ее объема, так как использоваться будет только ее малая часть, которую можно реализовать самостоятельно.

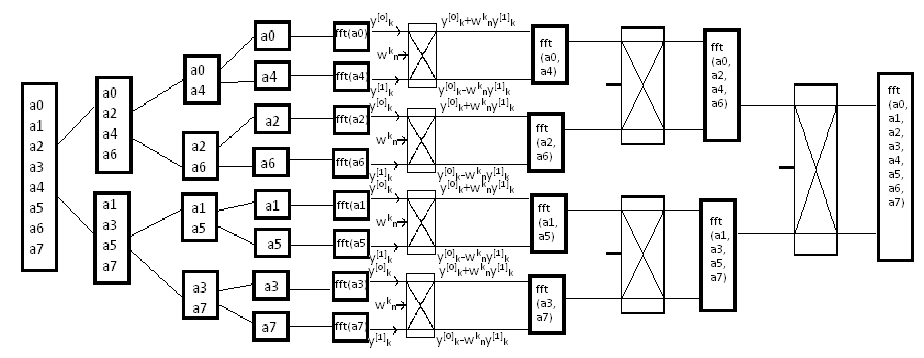
1. Алгоритм преобразования Фурье

Для ускорения получения результата реализован алгоритм быстрого преобразования Фурье (БПФ).

Были рассмотрены два варианта алгоритма [5]: рекурсивный и итерационный. Опишем их на алгоритмическом языке и затем проанализируем.

Рекурсивный алгоритм:

Recursive_FFT(a):

n = a.length //n является степенью 2

if n==1

return a

w_n= e^2iπ/n

w =1

a^[0] = (a₀, a₂, …, a_n-2)

a^[1] = (a₁, a₃, …, a_n-1)

y^[0] = Recursive_FFT(a^[0])

y^[1] = Recursive_FFT(a^[1])

for k = 0 to n/2 – 1

y_k = y^[0]_k + wy^[1]_k

y_k+(n/2) = y^[0]_k - wy^[1]_k

w = ww_n

return y

Итерационный алгоритм:

Iterative_FFT(a)

Bit_Reverse_Copy(a,A)

n = a.length //n является степенью 2

for s = 1 to lg(n)

m= 2^s

w_m= e^2iπ/n

for k = 0 to n – 1 by m

w = 1

for j = 0 to m/2 – 1

t = wA[k+j+m/2]

u = A[k+j]

A[k+j] = u+t

A[k+j+m/2] = u-t

w = ww_m

return A

Процедура Bit_Reverse_Copy размещает данные исходного массива a в массиве A в требуемом порядке, то есть осуществляет обратную перестановку или реверс битов. Например, если массив а=(0, 1, 2, 3, 4, 5, 6, 7), то на выходе получится массив А = (0, 4, 2, 6, 1, 5, 3, 7). Нумерация элементов меняется согласно правилу реверса битов.

Каждый алгоритм имеет вычислительную сложность θ(n lg(n)). При этом рекурсивный алгоритм разбивает исходный массив на части и сохраняет их копии, а итерационный копирует массив только один раз в требуемом порядке. Кроме того итерационный алгоритм требует вычисления lg(n) и округления его до целого числа, что так же задерживает выполнение преобразования.

В результате для реализации был выбран рекурсивный алгоритм.

Так как алгоритм рассчитан на отделение вычислительного модуля от ПК и библиотека математических вычислений не используется, возведение экспоненты в комплексную степень реализована через вычисление синуса.

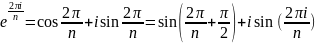
Для вычисления синуса разложим его в ряд Тейлора, для чего реализуем так же функцию возведения числа в степень и вычисление факториала.

Для работы с комплексными числами понадобится класс, реализующий их в алгебраической форме, а так же функции сложения, вычитания и умножения комплексных чисел.

Так как алгоритм рассчитан на количество отсчетов равное степени двойки, а на вход приходит кратное десяти, то перед началом преобразования дополним [6] сигнал нулями.

Продемонстрируем работу алгоритма для вектора из 8 элементов.