I. Основные термодинамические процессы

ИДЕАЛЬНОГО ГАЗА

I.I. Методика исследования термодинамических процессов

При изучении термодинамических процессов идеальных газов должны быть решены задачи:

первая - сводится к определению уравнения процесса устанавливаю­щего закономерность изменения состояния рабочего тела в процессе;

вторая - выявлению возможности преобразования подведенной к ра­бочему телу теплоты между изменением внутренней энергии и рабо­той, совершаемой рабочим телом.

Основой решения первой задачи является уравнение первого закона термодинамики, записанное согласно условий, присущих рассматриваемому процессу; и уравнение состояния идеального газа. Решение этих уравнений дает возможность получать соотношения различных параметров газа в виде  и ST. Вторая задача решается определением изменения внутренней энергии и работы. Изменение внутренней энергии для всех процессов определяется одинаково: du= , если известна теплоемкость . Внешняя работа и располагаемая работа L и определяются как: и

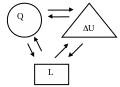О пределив эти величины, по уравнению первого закона термодинамики, определяют количество подведенной или отведенной теплоты. Характер преобразования теплоты в термодинамическом процессе удобно изображать в виде схемы, включающей три составные части уравнения первого закона термодинамики (рис.1).

Стрелками, связывающие эти три составные части, показаны лишь направление преобразования энергии. Они не затрагивают количественной стороны.

В общем случае в термодинамических процессах два параметра их трех могут изменяться произвольно. Однако изучение работы теплотехнических устройств показывает, что наибольший интерес для практики представляют следующие процессы изохорический, изобарический, изотермический, адиабатический и политропный.

Последний процесс при определенных условиях может рассматриваться в качестве обобщающего по отношению ко всем предыдущим термодинамическим процессам.

1.2 И30х0рный процесс.

Изохорный процесс происходит при нагревании или охлаждении газа в постоянном объеме. Подобный процесс может совершаться рабочим телом в резервуаре постоянного объема.

Уравнение изохорного процесса =const. Соотношение между параметрами состояния в процессе в соответствии с законом Шарля я идеальных газов будет

Работа газа при d=0 не совершается, т.е.

В PV – координатах изохорный процесс изображают отрезком прямой параллельной оси ординат (рис.2). При нагревании газа q0 его давление и температура повышаются, а при охлаждении q0 – уменьшается.

P 2

q0

1

q0

2

V

Рис. 2 PV - диаграмма изохорного процесса

Так как L=0, то подводимая к газу теплота идет на изменение его внутренней энергии. Поэтому в изохорном процессе с подводом теплоты внутренняя энергия газа и его температура повышаются, а с её отводом снижаются.

Принимая теплоемкость газа не зависящей от температуры, теплота изохорного процесса

Если теплоемкость в процессе переменная, то

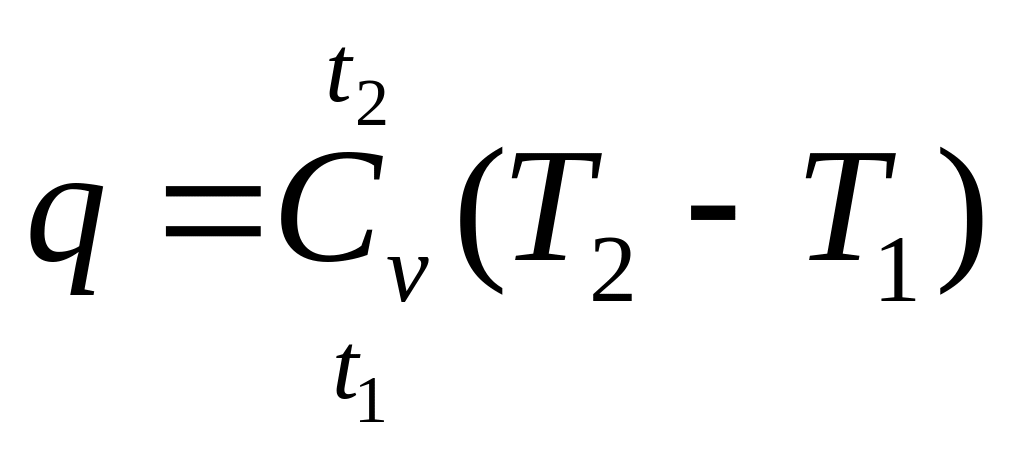
Для произвольного количества массы или объема газа

где 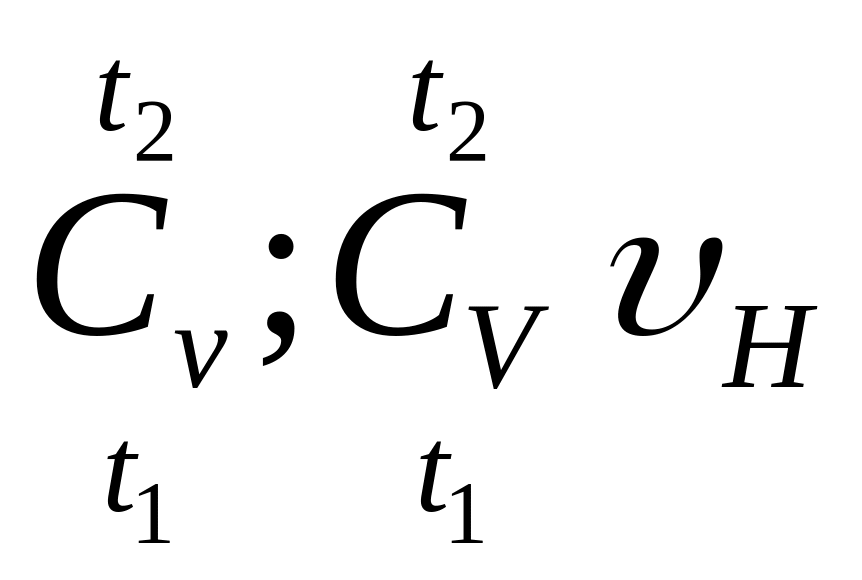- соответственно средняя массовая и объемная теплоемкость;

- объем, приведенный к нормальным физическим условиям;

М - масса газа. Изменение энтропии в изохорном процессе можно определить по выражению:

; если =const

то после интегрирования получаем:

Полученное соотношение показывает, что изохорный процесс в

T

Т

S - координатах является логарифмической кривой (рис.3) и протекает так, что с увеличением энтропии увеличи­вается температура.

Распределение тепло­ты в изохорном процессе выразится схе­мой (рис.4),которая показывает, что вся теплота подведенная к рабочему телу, расходуется на увеличение внутренней энер­гии.

Рис.4 Схема распределения теплоты в изохорном процессе.