
- •Энергия колебательной системы.
- •Затухание свободных колебаний
- •Вынужденные колебания при гармоническом внешнем воздействии. Резонанс колебаний
- •Переменный ток.
- •Явление резонанса.
- •Резонанс напряжений
- •Резонанс токов
- •Упругие волны. Поперечные и продольные волны.
- •Длина волны. Уравнение плоской бегущей волны.
- •Диапазоны электромагнитных волн.
- •Радиоволны
- •Видимое излучение (оптическое)
- •Энергия волны.
Энергия колебательной системы.
Энергия колебаний пружинного маятника:
![]() –
Энергия
колебаний – это сумма потенциальной
энергии пружины и кинетической энергии
груза.
–
Энергия
колебаний – это сумма потенциальной
энергии пружины и кинетической энергии
груза.
Формулы потенциальной и кинетической энергий:
![]()
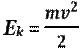
Затухание свободных колебаний
Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:
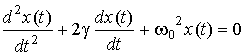 , (7.1.1)
, (7.1.1)
г
 де
де ![]() - коэффициент
затухания,
- коэффициент
затухания, ![]() - собственная
частота системы,
т.е. частота, с которой совершались бы
колебания в отсутствии затухания.
Выражение коэффициента затухания через
параметры системы зависит от вида
колебательной системы. Например, для
пружинного маятника
- собственная
частота системы,
т.е. частота, с которой совершались бы
колебания в отсутствии затухания.
Выражение коэффициента затухания через
параметры системы зависит от вида
колебательной системы. Например, для
пружинного маятника ![]() где r -
коэффициент сопротивления, т.е. коэффициент
пропорциональности между скоростью и
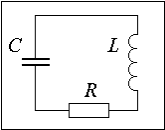
силой сопротивления. Для затухающих
колебаний в колебательном контуре
(рис.7.1.1):
где r -
коэффициент сопротивления, т.е. коэффициент
пропорциональности между скоростью и
силой сопротивления. Для затухающих
колебаний в колебательном контуре
(рис.7.1.1): ![]() ,
где R -
величина активного сопротивления
контура.
,
где R -
величина активного сопротивления
контура.![]()
Для
решения уравнения (7.1.1) производится
подстановка ![]() .
Эта подстановка приводит к характеристическому
уравнению:
.
Эта подстановка приводит к характеристическому
уравнению:
![]() , (7.1.2)
, (7.1.2)
которое имеет два корня:
![]() ,
, ![]() . (7.1.3)
. (7.1.3)
При
не слишком большом затухании (при ![]() )
подкоренное выражение будет отрицательным.
Если его представить в виде
)
подкоренное выражение будет отрицательным.
Если его представить в виде ![]() ,
где
,
где ![]() -
вещественная положительная величина,
называемая циклической частотой
затухающих колебаний и равная
-
вещественная положительная величина,
называемая циклической частотой
затухающих колебаний и равная ![]() ,
то корни уравнения (3) запишутся в виде:
,
то корни уравнения (3) запишутся в виде:
![]() и
и ![]() . (7.1.4)
. (7.1.4)
Общим решением уравнения (7.1.1) будет функция:
 (7.1.5)
(7.1.5)
которую можно представить в виде:
![]()
 , (7.1.6)
, (7.1.6)
Здесь ![]() и
и ![]() -
произвольные постоянные.
-
произвольные постоянные.
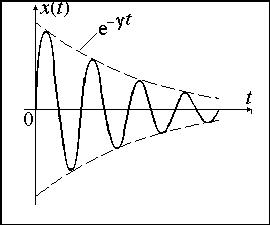
В соответствии с (7.1.6) движение системы можно условно рассматривать как гармоническое колебание частоты с амплитудой, изменяющейся по закону:
![]() . (7.1.7)
. (7.1.7)
С корость
затухания колебаний определяется
коэффициентом затухания
корость
затухания колебаний определяется
коэффициентом затухания ![]() .
В соответствии с выражением (7.1.7)
коэффициент затухания обратен по
величине тому промежутку времени, за
который амплитуда колебаний уменьшается
в «e»=2.718 раз. Период
затухающих колебаний определяется
формулой:
.
В соответствии с выражением (7.1.7)
коэффициент затухания обратен по
величине тому промежутку времени, за
который амплитуда колебаний уменьшается
в «e»=2.718 раз. Период
затухающих колебаний определяется
формулой:
 . (7.1.8)
. (7.1.8)
При
незначительном затухании (![]() )
период колебаний практически равен
)
период колебаний практически равен ![]() .
С ростом
период
увеличивается. Из соотношения (7.1.7)
следует, что
.
С ростом
период
увеличивается. Из соотношения (7.1.7)
следует, что ![]() . Такое
отношение амплитуд называется декрементом затухания,
а его натуральный логарифм - логарифмическим
декрементом затухания:
. Такое
отношение амплитуд называется декрементом затухания,
а его натуральный логарифм - логарифмическим
декрементом затухания:
![]() . (7.1.9)
. (7.1.9)
Логарифмический
декремент затухания обратен по величине
числу колебаний, совершаемых за то
время, за которое амплитуда уменьшается
в «e»
раз. Помимо рассмотренных величин для
характеристики колебательной системы
употребляется величина ![]() ,
называемая добротностью
колебательной системы.
Добротность пропорциональна числу
колебаний, совершаемых системой за то
время, за которое амплитуда колебаний
уменьшается в «e» раз. Большим значениям
добротности соответствует малое
затухание. Энергия колебательной системы
убывает со временем. Это обусловлено
наличием затухания. При малом затухании,
когда
,
называемая добротностью
колебательной системы.
Добротность пропорциональна числу
колебаний, совершаемых системой за то
время, за которое амплитуда колебаний
уменьшается в «e» раз. Большим значениям
добротности соответствует малое
затухание. Энергия колебательной системы
убывает со временем. Это обусловлено
наличием затухания. При малом затухании,
когда ![]() энергия
изменяется по закону:
энергия
изменяется по закону:
![]() , (7.1.10)
, (7.1.10)
где ![]() -
значение энергии в начальный момент.
-
значение энергии в начальный момент.
Можно показать, что при слабом затухании добротность с точностью до множителя 2 равна отношению энергии, запасенной в системе в данный момент времени, к убыли этой энергии за один период колебаний.
С
ростом период
колебаний увеличивается. При ![]() период
обращается в бесконечность, т.е. движение
перестает быть периодическим.
При
период
обращается в бесконечность, т.е. движение
перестает быть периодическим.
При ![]() выведенная
из положения равновесия система
возвращается в него, не совершая
колебаний.
выведенная
из положения равновесия система
возвращается в него, не совершая
колебаний.
