16 Вопрос.

Прямая геодезическая задача

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А(рис.23), горизонтальное расстояние S_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный уголα_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

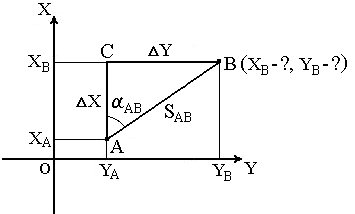
Рис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А( X_A, Y_A ), S_AB и α_AB.

Найти: точку В( X_B, Y_B ).

Непосредственно из рисунка имеем:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

ΔX = S_AB · cos α_AB ;

ΔY = S_AB · sin α_AB .

Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX  и  ΔY зависят от знаков cos α_AB  и  sin α_AB.

Знаки приращений координат ΔX и ΔY(Таблицу знаю)

При помощи румба приращения координат вычисляют по формулам:

ΔX = S_AB · cos r_AB ;

ΔY = S_AB · sin r_AB .

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

 X_B = X_A + ΔX  ;

 Y_B = Y_A + ΔY  .

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB (рис.24).

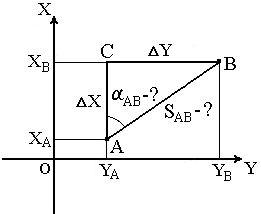
Рис. 24. Обратная геодезическая задача

Даннная задача решается следующим образом.

Сначала находим приращения координат:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Величину угла r_AB определем из отношения

ΔY	= tg rAB
ΔX

 .

 

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

SAB=	ΔX	=	ΔY	= ΔX · sec αAB = ΔY ·cosec αAB
	cos αAB		sin αAB

 

 

SAB=	ΔX	=	ΔY	= ΔX · sec rAB = ΔY ·cosec rAB
	cos rAB		sin rAB

Расстояние S_AB можно определить также по формуле

.

17 Вопрос.

Теодолит – это геодезический прибор, предназначенный для измерения горизонтальных и вертикальных углов. Бывают: Оптические, Электронные

Теодолит - довольно древнее изобретение. Он предназначен для измерения горизонтальных и вертикальных углов. Теодолит, является одним из основных измерительных приборов на любой строительной площадке. В зависимости от точности, теодолиты могут использоваться в триангуляции, полигонометрии, в геодезических сетях сгущения. Так же теодолиты нашли применение в прикладной геодезии, при проведении изыскательских работ. Кроме того, теодолиты применяют в промышленности при монтаже элементов конструкций машин и механизмов, строительстве промышленных сооружений и для выполнения других задач. Различают несколько основных типов теодолитов: Механический теодолит - теодолит с механической системой наведения и прицеливания (без оптических и электронных компонент). Оптический теодолит - теодолит, оснащенный оптическим отсчетным устройством. Электронный теодолит - теодолит, оснащенный микропроцессором и дисплеем для вычисления и запоминания координат точек на местности. По особенностям решаемых задач и дополнительного оснащения механические, оптические и электронные теодолиты можно разделить на следующие группы: астрономические, маркшейдерские (для тоннельных работ), военные, строительные и другие теодолиты. Оптические теодолиты оснащены оптической визирной трубой. В некоторых моделях считывание показаний осуществляется с вертикального и горизонтального лимба снаружи прибора (лимб открыт или есть визирное окно - встречается на учебных теодолитах), в других при помощи дополнительного визира, через который видно показания шкалы вертикального и/или горизонтального лимба. Высокоточные модели могут быть оснащены микрометрами для более точного наведения и считывания.

В настоящее время отечественными заводами в соответствии с действующим ГОСТ 10529 – 96 изготавливаются теодолиты четырех типов: Т05, Т1, Т2, Т5 и Т30.

Для обозначения модели теодолита используется буква "Т" и цифры, указывающие угловые секунды средней квадратической ошибки однократного измерения горизонтального угла.

По точности теодолиты подразделяются на три группы:

• технические Т30, предназначенные для измерения углов со средними квадратическими ошибками до ±30";

• точные Т2 и Т5 – до ±2" и ±5";

• высокоточные Т05 и Т1 – до ±1".

ГОСТом 10529 – 86 предусмотрена модификация точных и технических теодолитов. Так, например, теодолит Т5 должен изготовляться в двух вариантах: с цилиндрическим уровнем при алидаде вертикального круга и с компенсатором, заменяющим этот уровень. Теодолит с компенсатором при вертикальном круге должен обозначаться дополнительно буквой "К", например обозначается Т5К.

Технические и эксплуатационные характеристики теодолитов постоянно улучшаются. Шифр обновленных моделей начинается с цифры, указывающей на соответствующее поколение теодолитов: 2Т2, 2Т5К, 3Т5КП, 3Т30, 3Т2, 4Т30П и т.д.