mafh_2014_040

Форма № Н-9.02

Міністерство освіти і науки України

Чернівецький національний університет

імені Юрія Федьковича

. Факультет прикладної математики .

   Кафедра системного аналізу і страхової та фінансової математики  

Асимптотична поведінка важкої дифузійної частинки в потоці Арратья

Дипломна робота

ОКР «Магістр»

Виконала: студентка 5 курсу, групи 533       

Спеціальності 8.04020102 – актуарна та фінансова математика .

    Думитраш Христина Дмитрівна               

Керівник к.ф.-м.н. Конаровський Віталій Васильович  

Рецензент к.ф.-м.н. Попов Михайло Михайлович__________

Національна шкала                                                                                    

Кількість балів:                    Оцінка: ECTS                                             

Голова ДЕК ______________   д.ф.-м.н.  Маслюченко О.В. 

До захисту допущено:

Протокол засідання кафедри №      10    

від „    8    ”      квітня     2014 р.

зав. кафедри                          проф.Ясинський В.К.

Чернівці–2014

Анотація

В даній роботі розглядається система броунівських частинок зі склеюванням та досліджується еволюція важкої частинки в цій системі.

Зміст

Вступ……………………………………………………………………………4

Розділ I. Асимптотична поведінка важкої дифузійної частинки……….5

1.1. Система броунівських частинок зі склеюванням……………………5

1.2. Еволюція важкої частинки в системі броунівських частинок зі склеюванням………………………………………………………………..8

1.3. Асимптотичні властивості важкої частинки ……………………….12

Розділ II. Охорона праці та безпека у надзвичайних ситуаціях……….18

2.1. Правові, економічні і соціальні основи охорони праці…………....18

2.2. Поняття та види надзвичайних ситуацій. Правові основи забезпечення безпеки у надзвичайних ситуаціях……………………….21

2.3. Санітарно-технічні норми роботи з комп’ютерною технікою…….23

Висновки…………………………………………………………………...…28

Список літератури…………………………………………………………...29

Вступ

Дана модель взаємодіючих частинок є схемою до моделей, які вивчались Arratia R. [1] і Конаровським В.В. [4]. У роботі [1] побудовано систему броунівських частинок, що стартують з усіх точок числової прямої, рухаються незалежно до моменту зустрічі, потім склеюються і рухаються разом. Основною відмінністю є те, що у роботі розглядається наступна модель взаємодіючих частинок на прямій. Частинки стартують з цілих точок прямої, рухаються незалежно одна від одної до моменту зустрічі, потім склеюються і рухаються разом. Кожна частинка, яка стартувала не з початку координат, рухається як броунівська (не змінюючи своєї дифузії) до моменту зустрічі з частинкою, що стартувала з нуля. Частинка, яка стартувала з нуля, має масу і ця маса в момент часу 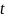рівна кількості частинок, що приклеїлись до неї до часу . Крім того коефіцієнт дифузії цієї частинки обернено пропорційно залежить від маси. Дану модель можна інтерпретувати наступним чином: ми поміщаємо в потік Арратья [1] важку частинку, яка при склеюванні з іншими частинками “сповільнює” свій рух (дифузія зменшується).

Дана дипломна робота складається з двох розділів. Перший розділ складається з трьох пунктів. У першому пункті побудовано систему процесів, яка описує еволюцію броунівських частинок, що стартували з цілих точок числової прямої, рухаються незалежно до моменту зустрічі, потім склеюються і рухаються разом. У другому пункті використовуючи побудовану систему вінерівських процесів із склеюванням (див. теорема 1) побудовано сукупність процесів, що описує поведінку даної системи процесів зі склеюванням. У третьому пункті досліджено асимптотичні властивості випадкового процесу 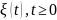. Зокрема встановлено закон повторного логарифму та доведено, що випадкові процеси склеюються за скінченний час. Другий розділ даної роботи присвячений охороні праці та безпеки у надзвичайних ситуаціях.

Розділ I. Асимптотична поведінка важкої дифузійної частинки