Пропорционально-интегральное регулирование.

Пропорционально-интегральное (изодромное) регулирование

При изодромном регулировании осуществляется регулирование по пропорциональному и интегральному принципам, т.е.

u(t)=K₁  (t) + K₂   (t) dt

Следовательно, изодромное регулирование призвано совместить высокую статическую точность интегрального регулирования с большим быстродействием пропорционального регулирования.

Часто уравнение ПИ-регулятора записывается в следующем виде

u(t)= К_п [  + (1/ Т_и)   (t) dt ],

где К_и - коэффициент пропорциональности ПИ-регулятора, а T_и - время изодрома или время удвоения.

Последнему выражению соответствует следующая передаточная функция регулятора

W_пи(p)= 

Такая передаточная функция в самом простом варианте может быть реализована на базе интегрального операционного усилителя в виде схемы (рис. 10.5)

Рис. 10.5.

Здесь: T_и = R₂ C, сек и K_и= R₂/R₁

Следовательно, логарифмические амплитудно- и фазочастотные характеристики можно изобразить в виде рис.10.6

Рис. 10.6.

 

 Поскольку ПИ-регулятор можно представить в виде параллельно включенных П-регулятора с коэффициентом передачи K_п и И-регулятора с коэффициентом передачи K_п/Т_и, реакция такого регулятора на единичный скачек ошибки или переходная характеристика может быть представлена в виде суммы реакций параллельных каналов, т.е

h(t)= h₁(t) + h₂(t) = К_п+(К_п/Т_и)t

где h₁(t)- реакция П-канала в виде скачка с амплитудой K_п , а h₂(t)-реакция И-канала в виде линейно возрастающей функции времени. Причем за время Т_ифункция возрастает на величину K_п. Поэтому постоянную времени интегрирования Т_и часто называют временем изодрома или временем удвоения . Сказанное иллюстрируется рисунком 10.7

Рис. 10.7.

 Детализированная структурная схема ПИ-регулятора представлена на рис.10.8.

Рис.10.8.

Математическую модель ПИ-регулятора составляют следующие уравнения

 =  ; U_у= y_и ( К_п/Т_и) + К_п .

Разложение в ряд Тейлора .

Дифференциальные уравнения системы записывают так, чтобы значения регулируемой величины и её производных располагались в левой части уравнения. Значения входных воздействий (управляющих и возмущающих) и их производных располагаются в правой части. При этом уравнение САУ имеет вид:

где a₀, a₁ … a_n — постоянные коэффициенты левой части уравнения; b₀, b₁ … b_m — коэффициенты правой части уравнения.

Значение выходной величины САУ обычно приводится к форме с единичным коэффициентом, т.е. коэффициенты уравнения делятся на a_n, b_m.

Обозначим операцию дифференцирования через символ дифференцирования:

иначе называемый алгебраизированным оператором дифференцирования — тождественно равно pⁱ). Это условная алгебраическая величина, представляющая собой функцию времени; р не обладает свойством коммутативности и является сомножителем только как py (px, pf и т.д.), но не yp (fp, p и т.д.).

Если пользоваться преобразованием Лапласа (или Карсона — Хевисайда) 1, с помощью которого рассмотрение процессов из временной области переносится в комплексную, тогда р будет являться комплексным числом p = c  j (иногда вместо р пишут S = c  j, о чём будет сказано ниже).

Определим уравнение динамики звена.

Рассмотрим нелинейное звено, входящее в структуру САУ, описываемое нелинейной функцией разложимой в ряд Тейлора в окрестности рабочей точки при внешнем возмущении f = 0:

. (8.1)

При работе САУ x и y мало отклоняются от их программных значений x₀, y₀, исходя из принципа работы замкнутой САУ. Следовательно,

, , , , ,

где  характеризует малые отклонения.

В установившемся состоянии уравнение нелинейного звена:

F(x, 0, y⁰, 0, 0)⁰ = 0 . (8.2)

Разложим уравнение (8.2) в ряд Тейлора:

. (8.3)

Далее, заменив частные производные коэффициентами, получим

где R_n определяет остальные члены порядка малости более двух (n > 2) и стремится к нулю при x  0 и y  0.

Вычитая из уравнения (8.3) уравнение (8.2), опустим знак  и, заменяя R_n на 0, получим линеаризованное уравнение в отклонениях:

или в операторной форме:

Следует заметить, что положение о малых отклонениях для возмущения f(t) обычно неприменимо, т.к. они могут иметь значительную величину.

Регулирование по производной.

Регулирование по производным

 

При регулировании по первой производной от ошибки осуществляется зависимость

u(t)= Kд d (t) / dt,

регулирующее воздействие (выходной сигнал регулятора) пропорционально скорости изменения ошибки. Это регулирование не имеет самостоятельного значения, т.к. в установившемся состоянии производная от ошибки равно нулю и регулирование пропадает. Однако оно может играть весьма большую роль в переходных процессах и вообще в динамике в качестве вспомогательного средства, так такое регулирование позволяет учитывать не только наличие ошибки, но и тенденцию к ее изменению (росту или уменьшению).

Логичным является формирование управляющего воздействия с учетом как самой ошибки, так и скорости ее изменения. Регулятор, реализующий такое управление носит название пропорционально- дифференциального или просто ПД- регулятора. Математически такой закон управления можно записать в виде

u(t)= K_п (t) + Kд d (t) / dt,

что позволяет представить структурно ПД-регулятор в виде параллельного соединения П- и Д- регуляторов с суммированием их управляющих воздействий.

В результате введение регулирование по производной от ошибки увеличивает скорость реакции системы регулирования, то есть повышает ее быстродействие, что приводит к снижению ошибок в динамике.

Часто передаточную функцию ПД-регулятора записывают в виде

W_пд(p)= K_п+ К_дp= K_п(T₁p+1)

Логарифмические амплитудно и фазочастные характеристики такого регулятора имеют вид

Рис.10.9.

 У идеального ПД-регулятора при воздействии единичной ступенчатой функции на его вход в момент времени t=0 на выходе появляется  - функция, имеющая известное аналитическое выражение

  при t=0

 (t)= 

 0 при t 0

Аналитическое переходная характеристики идеального ПД-регулятора рассчитывается по формуле

h(t)= K_п [ 1 +  (t) ] ,

а график ее представлен на рисунке 10.10.

Рис.10.10.

Формально ПД-регулятор может быть реализован на базе интегрального операционного усилителя по схеме рис.10.11

Рис.10.11.

 где K_п= - R₂/ R₁ и T₁=R₁C, сек.

Однако работа данной схемы сопровождается значительными высокочастотными помехами, для которых конденсатор C представляет собой сопротивление близкое к нулю. Для повышения устойчивости работы ПД-регулятора последовательно с конденсатором включается дополнительный резистор R3 с небольшим сопротивлением, которое ограничивает токи высокочастотных помех. Этот резистор на рисунке показан штриховой линией.

При наличии такого резистора передаточная функция регулятора приобретает вид

,

где T₁=(R₁+R₃)C, сек и T₂=R₃C, сек.

Таким образом регулятор приобретает инерционное звено первого порядка, что искажает амплитудно - и фазочастотную характеристику, как показано на рисунке 10.12.

Рис.10.12.

ЛАХ претерпевает излом на частоте  =1/ T₂ и фаза стремится к нулю при стремлении частоты к бесконечности. Естественно искажается и переходная характеристика регулятор- всплеск, соответствующий t=0, становится конечным и по амлитуде и по длительности. При стремлении R₃ к нулю ЛАХ стремятся к ЛАХ идеального ПД-регулятора, но практически никогда их не достигают. Проблема уменьшения влияния дополнительной инерционности возникает всегда при реализации ПД-закона регулирования на аналоговой элементной базе.

Детализированная структурная схема ПД-регулятора представлена на рис.10.13.

Рис.10.13.

 Математическую модель ПИ-регулятора составляют следующие уравнения

=  - y_и /Т₂;

U_у= y_и [ (К_п/Т₂)- (К_п Т₁/Т₂² )] + К_п Т₁/Т₂.

В некоторых случаях в закон регулирования могут вводиться производные более высоких порядков -вторая, третья и т.д. Это призвано улучшить динамические характеристики системы, однако техническая реализация введения производных выше второго порядка встречает значительные трудности.

Системы с ПД-регуляторами являются статическими и, следова-тельно, им свойственны с позиции статики все те же свойства и недостатки, что и для систем П-регуляторами. Устранение их достигается ведением регулирования по ПИД-закону.

Реальные дифференцирующее и интегрирующее звенья.

Реальное дифференцирующее звено

Передаточная функция:  .

Это произведение передаточных функций идеального дифференцирующего звена и апериодического звена. Если входная и выходная величина одной размерности, то передаточная функция записывается в виде:

где Т₁ – постоянная времени дифференцирующей части, Т₂ – постоянная времени инерционной части.

 

Уравнение звена

Найдем дифференциальное уравнение реального дифференцирующего звена. По определению передаточной функции:

Переходим от изображений к оригиналам:

Статическая характеристика: такая же, как у идеального дифференцирующего звена.

Переходная функция:    h(t)=   –  такая же, как весовая функция апериодического звена.

 

 

 

 

 

 

 

 

 

 

В отличие от идеального дифференцирующего звена у реального нет скачка до бесконечности при t=0. Инерционность сглаживает переходный процесс. Начальное значениеh(0) = K/T. Чем меньше Т, тем ближе звено к идеальному. Установившееся значение переходной функции равно нулю (она асимптотически приближается к этому значению).

 

ЛАЧХ и ЛФЧХ

Асимптотическая ЛАЧХ реального дифференцирующего звена состоит из двух прямых. Первая прямая проходит в диапазоне частот 0…1/T с наклоном +20 дБ/дек. Эта прямая (или ее продолжение) проходит на частоте ω=1 через значение 20lg(K).  Вторая прямая проходит в диапазоне частот 1/Т…∞ с наклоном 0 дБ/дек. Частота сопряжения этих прямых ω=1/Т.

Значения ЛФЧХ лежат в пределах +π/2…0 рад (+90º…0º). На частоте сопряжения φ(Т/2)= +π/4 рад (+45º). В области низких частот ω<<1/Т реальное дифференцирующее звено близко по своим свойствам к идеальному дифференцирующему звену W(p)=Kр, в области высоких частот ω>>1/Т реальное дифференцирующее звено близко по своим свойствам к пропорциональному звену W(p)=K/Т.

 

Пример ЛАЧХ и ЛФЧХ реального дифференцирующего звена для К<1, Т<1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Примеры реальных дифференцирующих звеньев

 

Реальный конденсатор

Как было показано выше, идеальный конденсатор (при R=0) можно представить идеальным дифференцирующим звеном с передаточной функцией W(p)=Cp. У реального конденсатора (R≠0) связь между током и напряжением описывается следующим уравнением:

Переходим к изображениям величин:

откуда получаем передаточную функцию реального конденсатора:

где величина RC – это постоянная времени. При R=0 получим передаточную функцию идеального конденсатора W(p)=Cp.

 

 

Резистивно-емкостный фильтр высоких частот

 

 

 

 

 

 

 

 

При скачке входного напряжения U₁ выходное напряжение U₂ в первый момент времени будет равно входному напряжению, а затем снижается по экспоненте до нуля (по мере заряда конденсатора и снижения тока в цепи конденсатора). Такой фильтр хорошо пропускает сигналы высоких частот (при ω>>1/T значение АЧХ близко к единице) и подавляет сигналы низких частот (при ω<<1/T значение АЧХ близко к нулю).

 

Механическая дифференцирующая система (демпфер-пружина).

 

 

 

 

 

 

 

 

 

Входной величиной будем считать перемещение поршня x, а выходной величиной – перемещение незакрепленного конца пружины y. Тогда такая система может быть описана как реальное дифференцирующее звено с постоянной времени дифференцирующей и инерционной части Т=δ/с (δ – коэффициент вязкого трения, с – коэффициент жесткости пружины)

 

 

 

 

 

При перемещении поршня в новое положение в первый момент времени конец пружины переместится на такое же расстояние, а затем возвращается в исходное положение. При движении поршня с постоянной скоростью (dx/dt=const) величина y будет постоянной и пропорциональной этой скорости.

 

Интегрирующее (астатическое) звено

 

Его уравнение , или , или py = ku.

Передаточная функция: W(p) = k/p.

Переходная характеристика:  (рис.44).

 

 

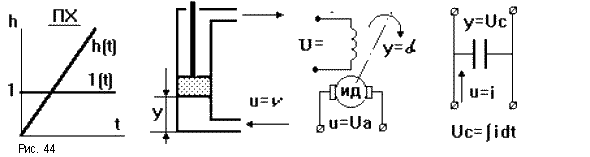
При k = 1 звено представляет собой “чистый” интегратор W(p) = 1/p. Интегрирующее звено неограниченно "накапливает" входное воздействие. Примеры интегрирующих звеньев: электродвигатель, поршневой гидравлический двигатель, емкость и т.п. Введение его в САУ превращает систему в астатическую, то есть ликвидирует статическую ошибку.

Составление дифференциальных уравнений звеньев и систем.