14. Интегральное регулирование.

Интегральный закон регулирования и соответствующий И - регулятор реализует следующую зависимость:

;

или

,

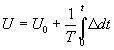где Т -постоянная времени интегрирования.

Недостатки: низкое быстродействие и нестабильность работы.

П люсы: отсутствует статическая ошибка.

Техническая реализация И - регулятора представляет собой усилитель постоянного тока с емкостной отрицательной обратной связью. И - регуляторы обеспечивают высокую точность в установившемся режиме. Вместе с тем И - регулятор вызывает уменьшение устойчивости переходного процесса и системы в целом.

Рассмотрим уравнение ошибки:

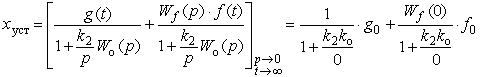
В установившемся режиме p→0, => W(p)→∞; => первая составляющая ошибки g₀/∞→0. Ошибка от возмущения зависит от вида функции W_f(0) и может быть отлична от нуля.

Обобщение: I-регулирование позволяет исключить статическую ошибку в системе, т.е. система будет астатической по отношению к задающему воздействию g(t).

Закон регулирования, которому соответствует передаточная функция

,

где Т_И – постоянная времени регулятора.

Здесь управляющее воздействие у в каждый момент времени пропорционально интегралу от сигнала ошибки е. Поэтому И - регулятор реагирует главным образом на длительные отклонения управляемой величины от заданного значения. Кратковременные отклонения сглаживаются таким регулятором.

Преимуществом данного регулятора является лучшая по сравнению с П - регулятором точность установки режима, а недостатками – худшие по сравнению с П - регулятором показатели качества, а именно большая колебательность и меньшее быстродействие.

14. Линеаризация. Практические рекомендации.

На практике все разнообразные по физическим свойствам систе­мы в большинстве случаев являются нелинейными, т. е. практически в системе присутствует одна или несколько нелинейностей. К ним относят люфт, упор, насыщение, ограничение и т.д. Анализ нели­нейных систем более сложен и, по существу, всегда является прибли­женным. Однако существует большой класс нелинейных систем, ко­торые при определенных допущениях можно линеаризовать, т. е. сис­тему сделать линейной в математическом смысле. При математи­ческом описании САУ обычно разбивают на ряд элементарных звень­ев, имеющих линейные статические характеристики, и на ряд звеньев с нелинейными статическими характеристиками. Линеаризация та­кой системы сводится к линеаризации уравнений, описывающих не­линейные звенья.

Методика составления линеаризованных дифференциальных урав­нений (по первому аналитическому способу линеаризации) сводится к следующему:

1. На основании изучения физических свойств реальной системы определяется число степеней свободы (число независимых переменных), производится ее декомпозиция и составляются исходные дифферен­циальные уравнения по звеньям.

2. Определяется рабочая точка установившегося режима работы звена (системы), в которой необходимо определить поведение звена (системы) при малых отклонениях от установившегося значения координат состояния (x⁰,y⁰)

3. Если в структуре САУ есть нелинейное звено, описываемое нели­нейной функцией

(2.1)

которая представляет собой несущественную нелинейность (анали­тическая нелинейная функция в области малых приращений), то ее можно разложить в ряд Тейлора в окрестности рабочей точки (0) при, например, внешнем возмущении f= 0.

4. В процессе управления в САУ в переходном и установившемся режимах х,у мало отклоняются от их программных значений х⁰, у⁰, исходя из принципа работы замкнутой САУ. Следовательно, для уравне­ния (2.1) можно записать, что 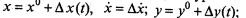, где знак ∆ характеризует малые отклонения (вариа­ции).

5. Уравнение нелинейного звена в установившемся состоянии:

(2.2)

6. Разлагая нелинейную функцию — уравнение (2.1) в ряд Тейлора, получим

или

где R_n определяет члены порядка малости; п> 2 (произведения и степе­ни малых отклонений с коэффициентами) — остаточный член, кото­рый стремится к нулю при

Из уравнения (2.3) вычитают уравнение (2.2) и, опуская знак ∆, рассматривают х, у уже в отклонениях, заменяя на нуль все после­дующие члены разложения как малые величины высшего порядка (R_n = 0). В результате получают линеаризованное дифференциаль­ное уравнение динамики звена в малых отклонениях:

или в операторной форме

Следует заметить, что положение о малых отклонениях для возму­щения f(t) обычно неприменимо, так как они могут иметь значитель­ную величину.

Отличие линеаризованного уравнения (2.4) от уравнения звена с нелинейной функцией (2.1) заключается в следующем: линеаризован­ное уравнение является приближенным, так как в нем отсутствуют члены высшего порядка малости; уравнение (2.4) записано только в отклонениях, т.е. неизвестными функциями времени являются не прежние полные величины (х, у), а их отклонения (∆х, ∆у), кото­рые характеризуют состояние звена в неустановившемся режиме (при отклонении от установившегося состояния с х⁰, y⁰); уравнение (2.4) является линейным относительно отклонений.

Частные производные здесь являются постоянными коэффициен­тами при отклонениях (или переменными коэффициентами, если F содержит t в чистом виде). Этот способ линеаризации справедлив для нелинейных функций, для которых возможно разложение в ряд Тейлора, т. е. когда функция F является аналитической в рабочей области (малые приращения).

Таким образом, уравнение (2.4) дает результат решения задачи линеаризации исходного уравнения (2.1), и его называют дифферен­циальным уравнением звена (или САУ) в отклонениях или «в вариа­циях».

Обычно практически линеаризацию производят сразу по анало­гии с уравнением (2.4), но не проводя предварительных выкладок (вто­рой способ). При этом используют графический смысл проведенной линеаризации.

Если статическая характеристика звена нелинейна, то ее часто называют характеристикой с переменным по входной величине коэф­фициентом передачи.

Известно, что решение дифференциального уравнения с определен­ными начальными условиями дает интегральную кривую.

Суть линеаризации состоит в замене кривой искомого решения нелинейного уравнения (2.1) прямой, касательной к искомой кривой в точке, соответствующей начальным условиям. Такая замена бу­дет, очевидно, справедливой только для тех отклонений ∆х, при которых кривая незначительно отличается от касательной. Следова­тельно, допустимая область отклонений и определяет возможности линеаризации исходной системы. При этом вместо частных произ­водных находят частные разности ∆у, ∆х.

Для уравнения (2.4) , когда выражения записаны в отклонени­ях, графически это будет означать перенос начала координат в точку О (рис. 2.9, б). Для реальных систем возможности такой линеаризации часто справедливы для достаточно больших значений отклонений; чем больше эти значения отклонений, тем больше к данным системам при­меним термин «линейные системы».

Основываясь на графической интерпретации способа линеариза­ции, примененяют способ графической линеаризации. Согласно ему, нелинейные статические характеристики линеаризуются графичес­ки, т. е. проводят касательную к кривой, соответствующей реальным условиям (рис. 2.9, кривая 7) и заменяют ее линеаризованной характе­ристикой (прямая 2). Тогда для малых отклонений система являет­ся линейной. При этом для упрощения знак «∆» перед переменны­ми опускают, предполагая, что эти переменные — малые отклоне­ния от установившегося состояния и линеаризация уже проделана. Следует заметить, что рассмотренная линеаризация уравнений совер­шенно недопустима при скачкообразных нелинейных функциях F (типа «релейных» характеристик). Такие функции и характеристики являются существенно нелинейными и изучаются в теории нелиней­ных САУ