Курсовая работа.

Дисциплина: Финансовый практикум.

Финансовый практикум

Задание

1. За сколько лет произойдет удвоение капитала при начислении сложных процентов раз в год по процентной ставке 0,14?

Решение:

П=П₀* (1,14) =1,14

=1,14

ответ - 5,3 лет

2. Покажите, что при фиксированной годовой процентной ставке r и сроке вклада, превышающем один год, начисление сложных процентов является более выгодным для вкладчика, чем начисление простых процентов.

Решение:

Простые проценты - проценты, начисляемы на первоначальную денежную сумму в течение всего периода начисления. Сложные проценты начисляются на денежную сумму и начисленные за предыдущий период проценты.

Рассмотрим на примере:

Пусть первоначальная сумма вклада составляет 150000 руб, срок вклада - 3 года, начисляемые проценты 40% годовых.

Определим наращенную сумму, используя простую и сложную ставку процента.

П = 150000 (1+0,4*3) = 330000 рублей.

П = 150000 (1+0,4) ⁿ

³ = 411600 рублей.

Таким образом, второй вариант расчетов, использующий сложную процентную ставку, очевидно, более выгоден для вкладчика, т.к. при начислении сложной процентной ставки происходит капитализация процентов, в данном случае ежегодно, на них, в свою очередь, также происходит начисление процентов.

3. Рассмотрите схему начисления сложных процентов несколько раз в год и сравните эффективную и номинальную ставки.

Решение:

Пусть сумма вклада 100000 рублей, процентная ставка - 8% годовых, начисление производится ежеквартально, т.е.4 раза в год, срок вклада - 3 года.

Номинальная ставка - это годовая ставка сложных процентов при одноразовом начислении процентов в году по фиксированной ставке.

П = 100000* (1,08) ³= 125971,2руб. В данном случае - 8%

Эффективная ставка - это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление в году по ставке, деленной на кол-во начислений в году.

П = По* (1+ ) ^m*n

П= 100000* (1+0,02) ¹²= 126824, 17 руб.

В данном случае эффективная ставка составляет 8,3%.

Начисление процентов несколько раз в году более выгодно для вкладчика, чем начисление 1 раз в год.

Для вычисления эффективной ставки в табличном процессоре есть финансовая функция ЭФФЕКТ (Номинальная ставка; Количество периодов).

ставка сложный процент кредит

Для вычисления номинальной ставки при заданной эффективной служит финансовая функция НОМИНАЛ (Эффективная ставка; Количество периодов).

Таким образом, эффективная ставка превышает номинальную.

4. Заемщик рассчитывает получить 14 % реального дохода от годового кредита с учетом ожидаемого темпа инфляции 12% в год. Какова должна быть ставка по кредиту?

Решение: В условиях инфляции кредиторы будут предоставлять кредиты по номинальной ставке процента (R), равной сумме реальной ставки процента (реальной доходности по кредиту) - r и ожидаемого темпа инфляции - π^e:

= r + π^e.

Найдем годовую ставку процентов, учитывающую инфляцию:

ia = i+a+i*a = 0,14+0,12+0,14*0,12= 0,2768

ставка по кредиту должна составлять 27,68%

5. При годовой ставке сложного процента r = 14% найдите современную и наращенную величины потока платежей

CF (1) = - 1120;

CF (2) =6272;

CF (3) = - 21952;

CF (4) =614656.

Решение:

Будущая сумма FV представляет собой сумму первоначального капитала PV и начисленного на него процентного дохода, получаемая в результате осуществления процесса наращения в течении n базисных периодов по ставке r.

Настоящая (текущая, современная) сумма денег представляет собой сумму будущих денежных поступлений, приведенных с учетом определенной ставки процента (так называемой дисконтной ставки) к настоящему периоду.

Пусть срок депозита - 4 года.

CF - выплата - величина периодического платежа

=FV/ (1+r) ⁿ

формула для нахождения современной величины потока платежей, где

FV - будущее значение, наращенное

PV - начальное значение вклада.

Выплаты за 4 года составляют FV = 597856 рублей.

PV = =353991,35 руб.

Современная величина = 353991,35 руб.

Наращенная величина = 597856 руб.

6. Найдите современную и наращенную величины 7 - летней ренты постнумерандо с ежегодным платежом 12 тысяч руб, если годовая процентная ставка r = 14 %. Ответы округлите до ближайшего целого числа.

Решение:

PV = 12000* = 12000*4,28 = 51428 руб

Таким образом, все будущие платежи оцениваются в настоящий момент в сумме 51428 руб. Иначе говоря, 51428 руб., размещенных под 14% годовых, обеспечивают ежегодную выплату по 12000 руб. в течение 7 лет.

При наращении всех платежей по той же ставке имеем

FV = 51428*1,14⁷ = 128570 руб.

7. Найдите выкупную цену бессрочной аренды, если ежегодная арендная плата составляет 120 тыс. руб., а годовая процентная ставка r = 14 %.

Решение:

В данном случае имеем дело с аннуитетными платежами.

Чтобы найти выкупную стоимость бессрочной аренды, аннуитет заменяют разовым платежом. Размер выкупа должен быть равен современной стоимости ренты: 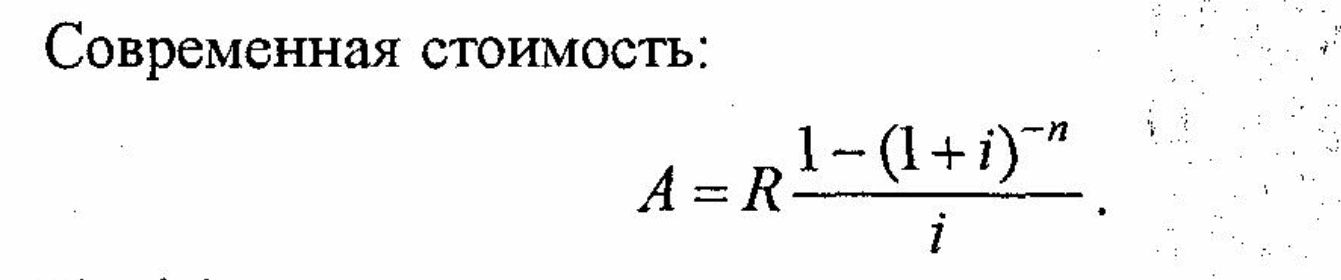, где сумма ежегодного платежа умножается на коэффициент приведения аннуитета.

Любая рента более 60 лет будет считаться вечной.

Коэффициент приведения аннуитета при i=0,14, n=60 будет равен 7,14.

А = 120000*7,14= 856812 тыс. руб.

Выкупная стоимость бессрочной аренды будет равна 856812 тыс. руб

8. Фонд учреждает стипендию в размере 24 тыс. руб. в год. Какую сумму для этого нужно внести в банк под 14 % годовых? Для защиты от инфляции предусмотрен постоянный годовой рост стипендии на 7%. Какую сумму в этом случае нужно положить в банк под 14% годовых?

Решение:

Чтобы ежегодные выплаты с банковского депозита вечно составляли 24 тыс. руб. в год, необходимо внести на депозит 171428,57руб.

Эквивалентная процентная ставка равна:

j = (1+i) - 1 = (1+ 0,14) - 1= 1,14 - 1 = 0,14

Приведенная величина вечного денежного потока может быть выражена действительным числом. Причем, формула ее определения очень проста:

где R - член ренты (разовый платеж), i - сложная процентная ставка.

А =R/j = 24000/0,14 = 171428,57 руб.

В случае, если член вечной ренты R ежегодно увеличивается с постоянным темпом прироста g, то приведенная стоимость такой ренты определяется по формуле: 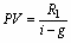PV = 24000/0,14-0,07 = 342857 руб

где R₁ - член ренты в 1-м году. Данная формула имеет смысл при g < i.