27.Векторы. Координаты вектора. Скалярное произведение векторов.

Отрезок, для которого указано какой из его концов считается началом, а какой концом называется вектором. Направление вектора отмечается стрелкой. Любая точка пространства может тоже рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают и он не имеет какого-либо определенного направления.

Длиной ненулевого вектора называется длина самого отрезка АВ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора коллинеарны и если при этом их лучи сонаправлены, то такие векторы являются сонаправленными, а если эти лучи имеют противоположное направление, то они противоположно направленные. Ненулевой вектор сонаправлен с любым вектором.

Единичный вектор – это вектор, длина которого равна единице. В пространственной системе координат существуют обозначения: вектор оси абсцисс, вектор оси ординат, вектор оси аппликат. Все эти векторы называются координатными векторами. Любой вектор можно разложить по координатным векторам, то есть представить в виде , причем различия определяются единственным образом.

Свойства координат вектора:

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Каждая координата разности двух векторов равна разности соответствующих координат векторов

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Каждая координата вектора равна разности соответствующих координат его конца и начала.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора равен квадрату его длины.

Длина вектора

28.Применение производной к исследованию функций и построению графиков (на примере нахождения монотонности).

Производная помогает во многих случаях сравнительно просто исследовать функцию на монотонность.

Пусть функция y = f(x) определена и непрерывна в промежутке х и во всех внутренних точках этого промежутка имеет неотрицательную производную, причем равенство f’(x) = 0 выполняется не более чем в конечном числе точке этого промежутка. Тогда функция возрастает на промежутке х.

Пусть функция y = f(x) определена и непрерывна в промежутке х и во всех внутренних точках этого промежутка имеет положительную производную причем равенство f’(x) = 0 выполняется не более чем в конечном числе точек этого промежутка. Тогда функция y = f(x) убывает на промежутке х.

Для нахождения промежутков монотонности функции нужно:

Найти производную функции

Приравнять производную к нулю и решить уравнение

Отметить на числовой прямой корни уравнения

Определить знаки получившихся интервалов и записать ответ

29.Использование координат векторов (точек) при решении математических задач(простейшие задачи в координатах).

А) Координаты середины отрезка. Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Б) Вычисление длины вектора по его координатам производится по формуле

В) Расстояние между двумя точками вычисляется по формуле

30.Функция y=sin(x), ее свойства и график.

Область определения – множество всех действительных чисел.

Область значение – отрезок [-1 ; 1]

Функция периодична. Основной период равен 2π.

Функция нечетная.

Функция возрастает на промежутках и убывает на промежутке , где n принадлежит множеству целых чисел.

31.Первообразная функции. Таблица первообразных элементарных функций. Основное свойство первообразной.

Функцию y = F(x) называют первообразной функции y = f(x) на промежутке х, если для любого х из Х выполняется равенство F’(x) = f(x).

Если F(x) первообразная для функции y = f’(x) на промежутке х, то у функции y = f(x) бесконечно много первообразных и все эти первообразные имеют вид F(x) + C, где С – любое действительное число.

Операцию отыскания первообразной называются операцией обратной дифференцированию.

Функция	Первообразная	Функция	Первообразная
k	kx + C	cos x	sin x
xr			-ctg x
	ln x + C		tg x
ex	ex + C		arssin x
	Ax		arctg x
sin x	cos x

Свойства первообразных:

Первообразная суммы равная сумме первообразных.

F (x) + H (x) = f (x) + h (x)

Постоянный множитель можно вынести за знак первообразной.

f (kx) = kF(x)

Если F(x) первообразная для f(x), а k и b – постоянные, причем k ≠ 0, то первообразная для f(kx+b).

32.Функция y=cos(x), ее свойства и график.

Область определения функции – множество всех действительных чисел.

Область значения – отрезок [-1; 1].

Функция периодическая с основным периодом 2π

Функция убывает на промежутках [2πn; π + 2πn] и возрастает на промежутках [- π + 2π; 2πn], где n принадлежит множеству целых чисел.

33.Интеграл. Определенный интеграл. Свойства.

Неопределенным интегралом от функции f(x), определенной на интервале (a;b) называют совокупность F(x) +C всех первообразных функции f(x), определенных не интервале (a;b) и обозначают ʃ f(x)dx = F(x) + C, где f(x) – подынтегральная функция, f(x)dx – подынтегральная выражение, х – переменная интегрирования, С – произвольная постоянная.

Приращение F(b) – F(a) любой из первообразных функций F(x) + C при изменении аргумента от x = a до x = b называется определенным интегралом от a до b функции f(x) и обозначается , где a и b – пределы интегрирования (a – нижний, b – верхний), [a;b] – отрезок интегрирования, f(x) – подынтегральная функция, x – переменная интегрирования.

Основные свойства определенного интеграла:

1⁰. Определенный интеграл с одинаковыми пределами равен 0:

2⁰. При перестановке пределов интегрирования знак интеграл меняется на противоположный:

3⁰. Отрезок интегрирования можно разбить на части: , где a < c < b.

4⁰. Постоянный множитель можно выносить за знак интеграла:

5⁰. Интеграл от алгебраический суммы функции равен алгебраической сумме интегралов от всех слагаемых: .

6⁰. Оценка определенного интеграла: если m ≤ f(x) ≤ M на [a; b], то m(b-a)M < < M(b-a).

Чтобы вычислить определенный интеграл, нужно:

Найти неопределенный интеграл от функции f(x), в котором можно принять C = 0;

В полученном выражении вместо аргумента х подставить сначала верхний предел b, а затем нижний предел a;

Из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.

Билет № 18

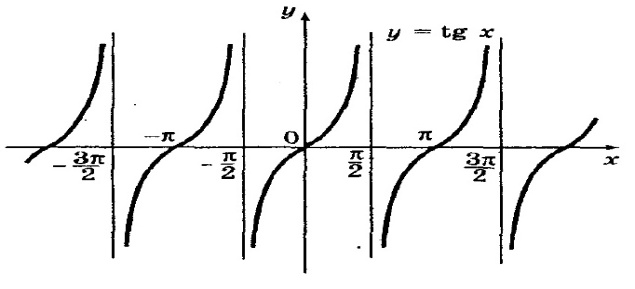
1.Функция y=tg(x) ее свойства и график.

Область определения , где k принадлежит к множеству целых чисел.

Область значений – вся числовая прямая.

Функция периодична с основным периодом π.

Функция нечетная.

Функция возрастает на промежутках .

36.Интеграл. Неопределенный интеграл. Свойства.

Неопределенным интегралом от функции f(x), определенной на интервале (a;b) называют совокупность F(x) +C всех первообразных функции f(x), определенных не интервале (a;b) и обозначают ʃ f(x)dx = F(x) + C, где f(x) – подынтегральная функция, f(x)dx – подынтегральная выражение, х – переменная интегрирования, С – произвольная постоянная.

Основные свойства неопределенного интеграла:

1⁰.Производная неопределенного интеграла равна подынтегральной функции .

2⁰.Дифференциал неопределенного интеграла равен подынтегральному выражению: d =

3⁰.Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

4⁰. Постоянный множитель можно выносить за знак интеграла: = a , где а – постоянная, а ≠ 0.

5⁰.Неопределенный интеграл от алгебраической суммы непрерывных функций равен алгебраической сумме интегралов от каждой функции: =

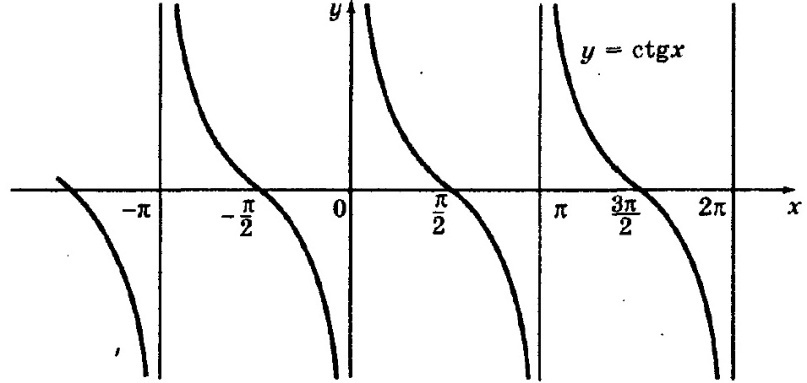
37.Функция y=ctg(x), ее свойства и график.

Область определения , где k принадлежит к множеству целых чисел.

Область значений – вся числовая прямая.

Функция периодична с основным периодом π.

Функция нечетная.

Функция возрастает на промежутках .

2.Теорема о вычислении площади криволинейной трапеции. Формула Ньютона-Лейбница.

Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона-Лейбница .Применяя обозначение F(b) – F(a) = F(x) , где F(x) – первообразная для f(x), формулу Ньютона-Лейбница запишем в виде

Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при вернем или нижнем пределах интегрирования. Вертикальная черта с верхним и нижним пределами, стоящая справа от символа функции F(x), называется знаком двойной подстановки.

Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.

Возможны следующие случаи:

Фигура ограничена графиком непрерывной и неотрицательной на отрезке [a; b] функции f(x) (f(x)≥0), осью Ox, прямыми x = a, x = b, тогда S =

Фигура ограничены графиком непрерывной и неположительной на отрезке [a; b] функции f(x) (f(x)≥0), осью Ox, прямыми x = a, x = b, тогда S =

Фигура ограничена осью Ox, прямыми x = a, x = b и графиком функции f(x), которая непрерывна на отрезке [a; b]и меняет свой знак конечное число раз на этом отрезке (Рис. 5). В этом случае разбивают отрезок [a; b] на такие частичные отрезки, на которых функция f(x) законопостоянна. Искомая площадь S численно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, причем знаки, с которыми эти интеграл входят в алгебраическую сумму, совпадают со знаками функции f(x) на соответствующих отрезках. Площадь фигуры, изображенной на рис. 5, вычисляется по формуле S=

38.Основные тригонометрические тождества, формулы приведения, примеры.

Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения).

Основные тригонометрические тождества

sin² α + cos² α = 1

tg α · ctg α = 1

tg α = sin α ÷ cos α

ctg α = cos α ÷ sin α

1 + tg² α = 1 ÷ cos² α

1 + ctg² α = 1 ÷ sin² α

Функция		Аргумент
sin		cos	cos	sin	-sin	-cos	-cos	-sin	sin
cos		sin	-sin	-cos	-cos	-sin	sin	cos	cos
tg		ctg	-ctg	-tg	tg	ctg	-ctg	-tg	tg
ctg		tg	-tg	-ctg	ctg	tg	-tg	-ctg	ctg

Заучивать эти формулы нет нужды. Достаточно помнить следующее:

1)  если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется;

если же в формуле  содержатся  углы  90° и 270° (^π/₂ и ^3π/₂), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.);

2)  чтобы определить знак в правой части формулы (+ или—), достаточно, считая угол  φ острым, определить знак  выражения, стоящего в левой части формулы.

39.Призма. Объем призмы.

Многогранник составленный из двух равных многоугольников (оснований), расположенных в параллельных плоскостях и n-параллелограммов (боковых граней) называется призмой. Отрезки боковых граней называются боковыми ребрами призмы. Ребра призмы равны и параллельных.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниями, то призма называется прямой. В противном случае наклонной. Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее основания правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.

S_полн. = S_бок + 2S_осн.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

S_бок = P·h.

Объем прямой призмы равен произведению площади основания на высоту.

V = S·h.

40.Тригонометрическое уравнение вида .

Формула для корней уравнения sin(x) = a, где -1,≤ а ≤ 1, имеет вид: x = (-1)^k + πk.

1) Нули синуса:

Уравнение можно решить

по общей формуле, однако наличие нуля в правой части делает ответ более удобным для дальнейшего отбора корней.

2) решение уравнения Sinx=1

Уравнение можно решить

по общей формуле, однако наличие единицы в правой части делает ответ более удобным для дальнейшего отбора корней.

3)решение уравнения SinX=-1

Уравнение можно решить

по общей формуле, однако наличие минус единицы в правой части делает ответ более удобным для дальнейшего отбора корней.

41.Цилиндр. Объем цилиндра.

Цилиндром (круговым цилиндром) называется тело, состоящее из двух кругов (оснований цилиндра)совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований.

Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра, такое сечение называется осевым. Площадь такого сечения равна площади прямоугольника, которая равна

Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение. Такое сечение называется сечением параллельным основанию.

Объем цилиндра равен числу π умноженному на квадрат радиуса одного из оснований и умноженного на высоту цилиндра.

V = πR²h.

42.Тригонометрическое уравнение вида .

Формула для корней уравнения cos(x) = a, где -1≤ а ≤ 1, имеет вид:  .

43.Пирамида. Объем пирамиды.

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину (вершину пирамиды) – точку пересечения отрезков (боковых ребер), соединяющих ее с вершинами основания.

Высотой пирамиды называется перпендикуляр, опущенный из ее вершины на плоскость основания.

В зависимости от многоугольника, являющегося основанием, пирамида может быть: треугольной, четырех угольной, пяти угольной, n-угольной.

Пирамида называется правильной, если в основании лежит правильный многоугольник, а ее высота проходит через основания. Все боковые ребра правильной пирамида равны; все боковые грани – равнобедренные треугольники. Высота боковой грани правильной пирамиды называется апофемой.

Тело, ограниченное сечением, проведенным в пирамиде параллельно основанию, основанием пирамиды, и заключенной между ними боковой поверхностью, называется усеченной пирамидой.

Объем пирамиды равен площади основания умноженной на высоту.

44.Тригонометрическое уравнение вида .

Формула для корней уравнения tg(x) = a имеет вид: x = arctg a + πk.

45.Конус. Объем конуса.

Конусом (круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с т очками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью прямого конуса называется прямая, содержащая его высоту.

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым. Площадью является площадь треугольника, которая равна половине произведения основания треугольника на его высоту. Основание данного треугольника будет равно диаметру основания конуса.

Если секущая плоскость перпендикулярна к оси конуса и параллельна его основанию, то сечение конуса представляет собой круг и называется сечением, параллельным основанию. Площадь такого сечения равна площади круга.

Для кругового и усеченного конуса имеются разные формулы объема.

Для кругового конуса .

Для усеченного конуса .

46.Тригонометрическое уравнение вида .

Формула общего решения уравнения ctg x = a при любом действительном а имеет вид x = arcctg a + πn.

47.Событие (случайное, достоверное, невозможное, несовместное, равновозможное, независимые).

Теория вероятности – это раздел математики, изучающий закономерности массовых случайных событий. Случайным событием называется факт, который в результате опыта может произойти или не произойти. Случайным называется событием, наступление которого гарантировать нельзя.

Достоверным называется такое событие, которое в данном опыте произойдет обязательно.

Невозможным называется событие, которое в данном опыте не может произойти.

Событие – это факт, который при осуществлении определенных условий может произойти или нет. Событие обозначают большими буквами латинского алфавита.

События называют несовместимым, если в результате испытания появление одного их них исключает появление другого. События называют совместными, если в результате испытания появление одного из них не исключает появление другого.

События называют равновозможными, если у них равны возможности появления.

Два события а и b называют независимыми, если появление одного из них не влияет на появление другого.