39. Неравенство Чебышева. Закон больших чисел (теорема Чебышева). Теорема Маркова.
Пусть существует некоторая
случайная величина X,
для которой
.
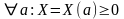Тогда если
,
то для любого
верно
.
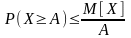Из этого неравенства можно получить
неравенство Чебышева:
.
Иными словами, случайная
величина принимает значения, близкие
к своему среднему.
Теорема Чебышева (закон
больших чисел): Пусть
имеются некоторые попарно независимые
случайные величины
.
Если
,
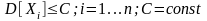то при любом A>0
верно, что
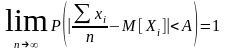- при большом числе опытов среднее
арифметическое приближается к мат.
ожиданию.
Закон больших чисел может
быть распространен и на зависимые
случайные величины. Такое обобщение на
случай зависимых случайных величин
носит название теоремы
Маркова: если для
зависимых случайных величин
,
то
.
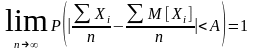40. Закон больших чисел и центральная предельная теорема.
Закон больших чисел в той или
иной форме показывает только то, что
случайные величины сходятся по вероятности
к тем или иным постоянным. Однако они
ничего не говорят о возможном распределении
случайных величин. Для установки условий,
при которых случайная величина подчиняется
нормальному закону распределения,
существует целый набор центральных
предельных теорем:
пусть некоторая исследуемая величина
Х может
быть представлена как сумма независимых/слабо
зависимых (ни одна из величине вносит
серьезного вклада в значение величины
Х)
величин
.
Пусть также мат. ожидания
и дисперсии
конечны. Тогда
.
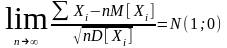На практике (например, в теории стрельбы) случайные величины (ошибка стрельбы) состоят из множества слабо зависимых случайных величин (набор элементарных ошибок), каждая из которых вносит небольшой вклад в общую ошибку, поэтому, закон распределения этих случайных величин может быть представлен как стандартный закон распределения.
42. Характеристические функции. Теорема Ляпунова. Теорема Лапласа.
Характеристическая функция
случайной величины Х
– функция
,
являющаяся мат. ожиданием комплексной
случайной величины
.
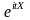Если Х
– дискретная случайная величина, то
,
если же величина непрерывная, то
.
Т.к. функция
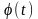выражается из функции
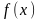через преобразование Фурье, то функция
выражается из функции
через обратное преобразование Фурье:
.
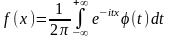Характеристические функции применяются
для композиции законов
распределения: если
существуют случайные величины
с плотностями распределения
,
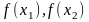то плотность распределения величины
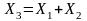может
быть найдена как
.
Теорема Ляпунова используется, когда требуется доказать, что случайная величина, полученная как сумма большого числа независимых случайных величин, подчиняется нормальному закону распределения: пусть ля попарно независимых случайных величин выполняются условия:
1)
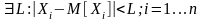(значения всех случайных величин
равномерно ограничены относительно
мат. ожиданий).
2)
.
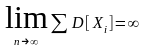Тогда при достаточно большом
числе n величина
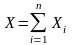распределена нормально с
,
,
.
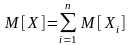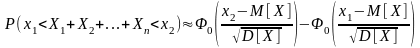Теорема Лапласа
Пусть выбраны любые
строк
матрицы
.
Тогда определитель матрицы
равен
сумме всевозможных произведений миноров
-го
порядка, расположенных в этих строках,
на их алгебраические дополнения.
где суммирование ведётся по
всевозможным номерам столбцов
