31. Равномерное распределение, экспоненциальное распределение, гамма-распределение.

Равномерное распределение на отрезке [a;b] характеризуется постоянной плотностью 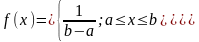на интервалах. Для этого распределения , , .

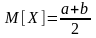Показательное распределение с параметром и плотностью 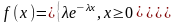и функцией распределения является аналогом закона Пуассона для непрерывных случайных величин. В этом случае , , . .

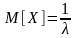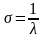Гамма-распределение с параметрами 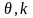и, иногда, сдвигом, задается плотностью 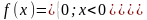, где - гамма-функция Эйлера. Для гамма-распределения , .

32. Нормальный закон распределения и его график. Интеграл вероятности, его свойства и график. Интеграл . Смысл параметров. Стандартное нормальное распределение. Моменты нормального распределения.

Нормальное распределение с мат. ожиданием m, среднеквадратичным отклонением 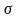и плотностью является наиболее часто встречающимся на практике законом распределения. Оно является предельным законом и при соответствующих условиях переходит в другие виды распределения. Часто использую стандартный вид нормального распределения с 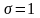, m=0.

Мат. ожидание m – центр симметрии (задает смещение графика по оси ОХ), среднеквадратичное отклонение задает форму кривой (её вытянутость по оси ОУ).

Для нормального распределения , 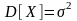. Кроме того, существует простая рекуррентная формула для нахождения моментов 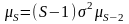. Т.к. , то все нечетные моменты нормального распределения равны нулю, для всех нечетных чисел выполняется соотношение .

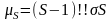Функция 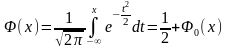называется интегралом вероятности и она показывает распределение стандартизированной нормальной величины. Эта функция с точностью до масштаба и сдвига совпадает с нормальным распределением. Отсюда легко заметить, что вероятность того, что случайная величина X примет значение в интервале 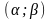равна 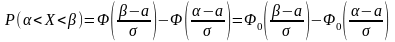. При этом .

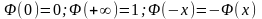33. Правило трех сигм.

Правило трех сигм – отклонение значений случайной величины, распределенной нормально, от своего среднего значения практически не превосходит утроенного среднеквадратичного отклонения.

34. Понятие о системе случайных величин. Функция распределения системы случайны величин.

Иногда при изучении случайных явлений приходится оперировать не одной, но двумя и более случайными величинами. В этом случае говорят, что если на пространстве элементарных событий заданы n случайных величин 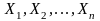, то задана n-мерная случайная величина (n-мерный случайный вектор) 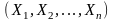. В случае изучения параметров системы случайных величин недостаточно изучать отдельно случайные величины - нужно также учитывать связи между ними.

Закон распределения системы случайных величин - соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях. Функцией распределения n-мерной случайной величины называется функция .

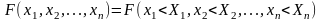Свойства функции распределения системы случайных величин:

1) .

2)

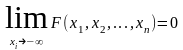
3) Функция 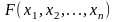является неубывающей.

4) Зная функцию распределения системы случайных величин легко можно найти закон распределения случайной величины как .
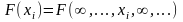