10. Сумма событий. Теорема сложения вероятностей.

Сумма группы событий – событие, состоящее в появлении хотя бы одного из событий (аналог логического ИЛИ).

Теорема сложения вероятностей – вероятность суммы событий равна сумме вероятностей событий минус вероятность произведения событий, т.е. . Если события несовместны, то , т.е. (это правило легко обобщить на n несовместных событий: ). Отсюда следует, что сумма вероятностей противоположных событий равна 1 и вероятность суммы событий, образующих полную группу несовместных событий, равна 1.

11. Вероятность противоположного события.

Для любого события А существует вероятность противоположного событи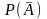я , равная .

12. Условная вероятность.

Условная вероятность события А при наличии В – вероятность события А, вычисленная при условии, что событие В произошло. Записывается как 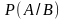. Если А, В – независимые события, то , в противном случае события зависимые ( ).

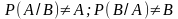13. Произведение событий. Теорема умножения вероятностей.

Произведение группы событий – событие, состоящее в совместном проявлении всех событий (аналог логического И).

Вероятность произведения событий А, В – вероятность одного из них умноженная на условную вероятность второго при наличии первого, т.е. . Если события А и В независимы, то .

14. Формула полной вероятности.

Пусть событие А может произойти только с одним из гипотез, образующих полную группу несовместных равнозначных событий. Тогда . Эта формула носит название полной вероятности.

15. Теорема гипотез (формула Байеса).

Формула носит название формулы Байеса. Она позволяет по заранее известным вероятностям гипотез 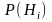с учетом наблюдавшегося результата А найти вероятность для любой из гипотез .

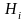16. Последовательность испытаний. Частная теорема о повторении опытов.

Несколько опытов называются независимыми, если вероятность каждого из опытов не зависит от предыдущих. Последовательность испытаний – такая серия испытаний, в которой некоторое событие А может наступить с фиксированной вероятностью.

Формула Бернулли (частная теорема о повторении опытов): пусть проводится n независимых опытов. Вероятность наступления некоторого события A одинакова и равна P. Тогда вероятность того, что событие A произойдет в n опытах ровно m раз равна .

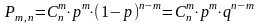17. Общая теорема о повторении опытов. Схема Бернулли.

Общая теорема о повторении опытов: пусть проводится n независимых опытов, причем вероятность события A в i-м опыте равна 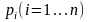. Тогда вероятность того, что событие А повторится в n опытах ровно m раз равна коэффициенту при 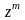в разложении по степеням z производящей функции .

18. Формула Пуассона.

Формула Бернулли удобна для вычисления при достаточно небольшом числе n. В противных случаях используют теорему (формулу) Пуассона: если при достаточно большом числе опытов n вероятность наступления события A p достаточно мала, то вероятность наступления события A ровно m раз равна .

19. Локальная теорема Муавра-Лапласса.

В случае же, когда n, m достаточно большие, а p и q не близки к нулю (должно выполняться условие ), то для нахождения вероятность наступления события A ровно m раз используют локальную теорему Муавра-Лапласса: 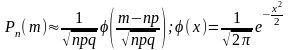. Обычно таблицы для нахождения значений функции 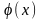приводятся в справочниках, кроме того, .

20. Интегральная теорема Муавра-Лапласса.

Если же требуется найти вероятность наступления события A в n опытах не меньше 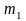раз и не больше 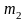раз, то используется интегральная теорема Муавра-Лапласса: 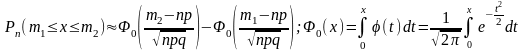. Таблицы для нахождения значений 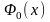обычно приводятся в справочниках, при этом , .

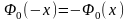21. Ряд распределения. Многоугольник распределения. Функция распределения и её свойства.

Случайная величина Х – величина, которая при проведении опыта принимает неизвестное заранее числовое значение. Случайные величины могут быть как дискретными (её значения образуют конечный/бесконечный ряд чисел 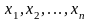и каждому такому значению можно поставить в соответствие вероятность ), так и непрерывными (значения случайной величины занимают конечный/бесконечный промежуток (a;b)).

Ряд распределения дискретной случайной величины Х – таблица, в которой перечислены различные возможные значения случайной величины и соответствующие им вероятности . При этом . Многоугольником распределения называется графическое представление ряда распределения.

Понятие ряда/многоугольника распределением может быть сформулировано только для дискретной случайной величины. В случае же непрерывной величины используется не равенство X=x, а неравенство X<x, т.е. формулируется понятие функции распределения.

Функция распределения случайной величины Х – функция 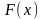, выражающая вероятность того, что случайная величина X примет меньшее, чем х, значение, т.е. 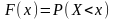. Функция распределения существует как для непрерывных, так и для дискретных величин (в этом случае она будет являться разрывной кусочной функцией).

Общие свойства функции распределения:

1) - функция распределение является неубывающей функцией.

2) .

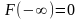3) .