1. Предмет теории вероятностей. Краткие исторические сведения. Случайная величина. Практически невозможные и практически достоверные события.

Предмет теории вероятностей – изучение законов, управляющих случайными событиями. Началом работ по теории вероятностей считается начало17 века (Галилей, исследуя ошибки в своих опытах, отметил их как случайные), в это же время возникает и тория страхования. Однако окончательно наука сформировалось несколько позже для описания азартных игр (работы Паскаля, Ферма и Гюйгенса) – в их работах сформированы понятия вероятности и мат. ожидания и разработаны методы их нахождения. Бернулли осуществил первое доказательство закона больших чисел (в дальнейшем в работах Пуассона, Чебышева и др. этот закон непрерывно дорабатывался, расширялись границы его применимости). Муавр ввел понятие нормального (Гауссово) распределения, сформировал центральные предельные теоремы. В работах Лапласа появилось строгое изложение основ теории вероятности и доказательство одной из форм ЦПТ (теорема тоже в дальнейшем доказывалась для более общих случаев многими учеными). Гаусс обобщил понятие нормального распределения и разработал метод обработки экспериментальных данных – метод наименьших квадратов. В 30г. 20 века в Западной Европе происходит угасание интереса к теории вероятности, однако она обширно изучается в России – создается Петербургская математическая школа. Её выпускниками были Буняковский (автор первого курса теории вероятности на русском языке, создатель первой русской терминологии), Чебышев (разработал метод моментов), Марков (заложил основы теории стохастических процессов), Ляпунов (разработал метод характеристических функций) и многие другие.

Событием называется всякий факт, который в результате испытания может произойти или не произойти. Достоверное/недостоверное событие U/V – событие заведомо произойдет/не произойдет в результате испытания. Их вероятности равны единице и нулю соответственно. На практике же приходится иметь дело не с достоверными/недостоверными событиями, а с практически достоверными/невозможными событиями – их вероятности соответственно практически равны единице/нулю. В теории вероятностей очень важной задачей является поиск условий, при которых событиях становятся практически достоверными/невозможными.

Испытание – реализация данного комплекса условий, в результате которого непременно произойдет какое-либо событие. Совокупностью элементарных событий является пространство элементарных событий .

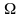Случайная величина в результате опыта может принять то или иное значение (т.е. заранее оно не известно). Случайные значения принимают либо дискретный, либо непрерывный характер.

2. Размещение с повторениями и без повторений. Примеры.

Размещением m элементов из n элементов – число упорядоченных наборов из m элементов, взятых из n элементов. Находится по формуле .

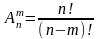Размещением с повторениями m элементов из n элементов – число упорядоченных наборов из m элементов, взятых из n элементов, причем, в элементы в наборах могут повторяться. Находится по формуле .
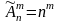