11. Ваше понимание особенностей случайного процесса Маркова (марковского процесса).

Случайная величина позволяет представить поведение изменяющегося случайным образом сигнала в определенный момент времени. Однако при проектировании целого ряда систем связи важно учитывать изменение случайных сигналов не только по уровню, но и во времени. В качестве моделей случайных сигналов и помех, позволяющих отразить их динамические характеристики, используются случайные процессы (СП), представляющие собой случайные функции времени. При этом конкретный вид, который принимает СП в отдельном эксперименте, называется реализацией СП [4, 6]. Во многих радиотехнических приложениях СВ   связаны со значениями непрерывного процесса    в моменты времени  , т. е.  . В этом случае упорядоченная система непрерывных СВ   (рис. 3.1) называется случайной последовательностью, которую можно также интерпретировать как реализацию СП в данном опыте [5].Простейшее вероятностное описание СП соответствует независимым СВ  , тогда совместная ПРВ  .

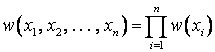12. Объясните кратко понятие и сущность уравнений Колмогорова как метода математической физики.

Полно:

Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы S Из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлении и т. д.). Если все потоки событий, переводящие систему S из состояния в состояние,—простейшие, то процесс протекающий в системе, будет марковским). Это и естественно, так как простейший ноток не обладает последействием: в нем «будущее» не зависит от «прошлого».

12.2 В самом деле, пусть рассматривается система S, имеющая n возможных состояний (S₁, S₂,…. S_n). Назовем вероятностью i-ого состояния вероятность p_i(t), того, что в момент t система будет находиться в состоянии S_i. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:

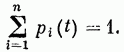
Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний p_i(t)  как функций времени. Для этого составляются и решаются так называемые уравнения Колмогорова — особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.

12.3 При составлении уравнений Колмогорова по графу состояний

При составлении уравнений Колмогорова по графу состояний удобно ввести понятие «поток вероятности». Будем называть потоком вероятности, переводящим систему из состояния Si, в состояние Sj ,; произведение вероятности pi(t) состояния Si из которого исходит стрелка, на интенсивность λ_ij потока событий, переводящего систему по этой стрелке.

Уравнения Колмогорова составляются по следующему мнемоническому правилу: производная вероятности любого состояния равна сумме потоков вероятности, переводящих систему в это состояние, минус сумма всех потоков вероятности, выводящих систему из этого состояния.

12.4 Пример нахождения вероятности по уравнениям Колмогорова:

Рис.1 Пример простейшего графа состояний

Для такого графа уравнения Колмогорова будут иметь вид:

,

Решение (находим вероятности). Нормировочное условие: p₁(t)+p₂(t)=1, откуда p₂(t)=1-p₁(t) (2)

Подставим выражение (2) вместо значения вероятности p₂(t)в первое из уравнений (1) .

В результате такой подстановки получим одно дифференциальное уравнение с одной неизвестной функцией p₁(t):

_{Или приводя подобные}

Решая это линейное дифференциальное уравнение с переменным коэффициентами λ(t) и μ(t) получим сложное решение.

_{Рассмотрев для простоты частный случай, когда интенсивности λ(t) и μ(t) не зависят коэффициентами λ(t)= λ=const и μ(t)= μ=const получаем уравнение (3) при λ(t)=λ, μ(t)=μ при начальном условии p1(0)=1:}

₍₃₎

_{Интегрируя это уравнение, получим:}

_Откуда