Вопросы к экзамену по ММФ в НГД

1. Дайте кратко описания физических задач сводящихся к линейным дифференциальным уравнениям с частными производными второго порядка, в частности, для случая, когда искомая функция зависит от двух независимых переменных.

Ответ:

Физические задачи о:

1. Поперечных колебаниях струны (струй, растяжек);

2. Продольных колебаниях стержней (буровых колонн);

3. Звуковых и электромагнитных колебаниях;

4. Колебаниях газа (газа в резервуаре);

5. Фильтрации жидкостей или газов;

6. Распространении тепла в однородной среде (буровая колонна);

7. Стационарном распределении тепла в однородном теле;

8. Потенциале скорости безвихревого движения и другие задачи о свойствах стационарных (установившихся) процессов.

2. Назовите основные уравнения математической физики для случая искомой функции зависящей от двух независимых переменных.

Ответ:

1. Волновое уравнение 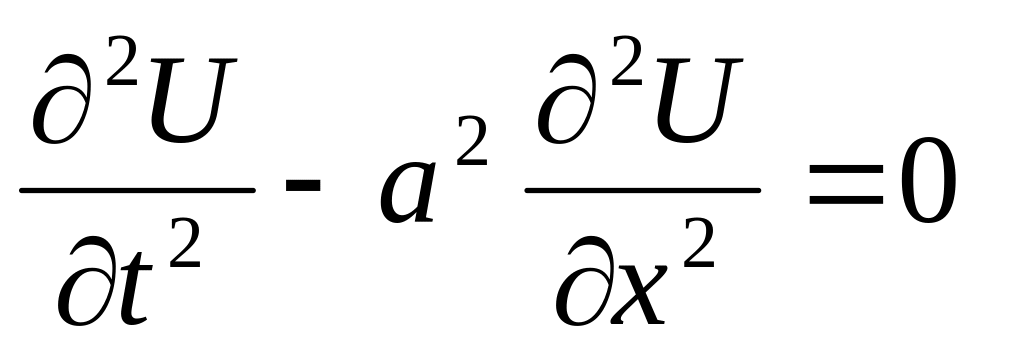– простейшее уравнение с частными производными второго порядка гиперболического типа.

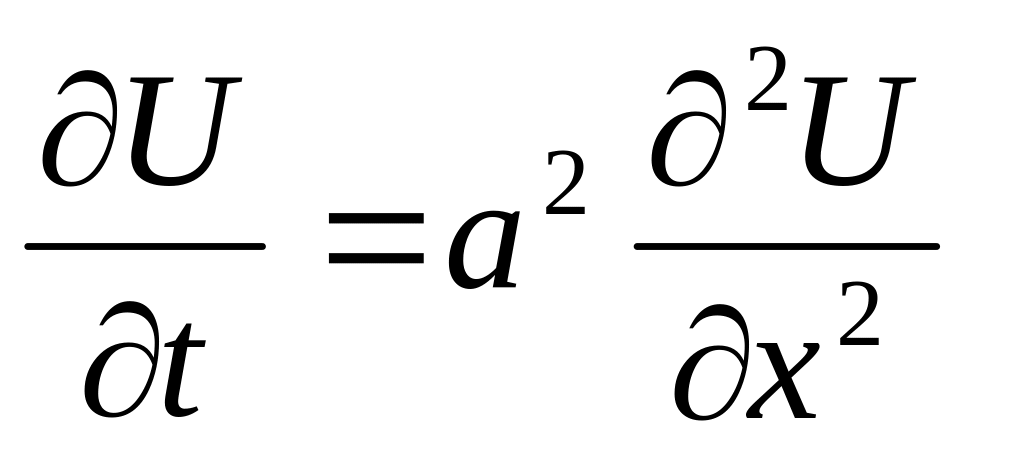2. Уравнение теплопроводности - простейшее уравнение с частными производными второго порядка параболического типа.

3. Уравнение Лапласа - простейшее уравнение с частными производными второго порядка эллиптического типа.

3. Изложите кратко сущность метода Фурье при решении задач разработки нефтяных и газовых месторождений методами математической физики. Ответ: Сначала ищутся частные решения в виде произведения функций, каждая из которых зависит только от одного аргумента. Затем, исходя из заданных краевых условий, определяются значения произвольных постоянных, содержащихся в этих частных решениях. В результате искомое решение, удовлетворяющее данному решению и данным краевым условиям, получается в виде ряда, составленного из найденных частных решений, или в виде несобственного интеграла с бесконечными пределами.

4. Основные определения и понятия фрактальной геометрии и фрактальной размерности. Фрактал - это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, строго большую топологической. Масштабная инвариантость, наблюдаемая во фракталах, может быть либо точной, либо приближённой, а сама размерность-фрактальная.Структуры, которые ведут себя как фрактальные на масштабах l<R, получили название однородные. Фрактальную размерность иногда называют дробной размерность. Однако дробность D не является необходимым условием фрактальности. Существуют фрактальные объекты, размерность D которых выражается целым числом. Ключевым в определении фрактала является условие Мандельборта D>dт.

5. Поясните формальное определение самоподобия и ваше понимание возможностей фрактальной геометрии как метода математической физики при решении задач разработки нефтяных и газовых месторождений. Понятие самоподобия состоит в том, что на каждом шаге представленном на рисуке, при увеличении проивзольного выделенного участка кривой в n раз, мы получаем кривую близкую к исходной. Каждая из таких кривых не повторяет исходную абсолютно точно. Но усреднив все полученные в результате, мы как раз получим исходную линию.

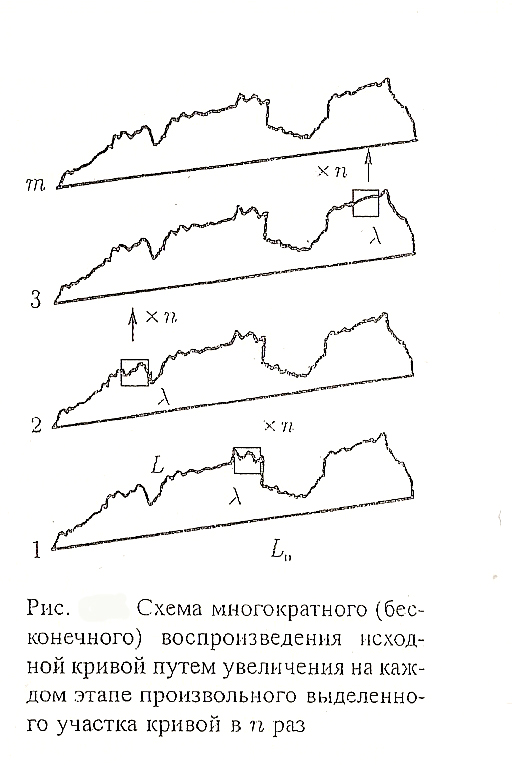
Фрактальный метод при решении задач разработки нефтяных и газовых месторождений:

• Фрактальный анализ динамики давления в скважине - неравномерное распределения давления в трещинах пласта. Установлено, что колебания давления на забое фонтанных скважин имеют детерминированный характер

• Образование фрактальных структур в пористых средах (трещины, каверны)

6. Совместимы ли подходы кластерного и фрактального анализа при решении задач с использованием методов математической физики.

Подходы кластерного и фрактального анализа применимы для решения задач нефтяной геологии. Они могут применятся как по отдельности так и в комплексе, например с помощью фрактального анализа описываются структуры порового пространства, а с помощью кластерного анализа полученные данные можно объединить в группы, с одинаковыми структурами порового пространства, тем самым провести корреляцию пластов с одинаковыми свойствами.