2.2.2.Процес дешифрування.

Підблоки ключа при дешифруванні є одночасно як адетивними так і мультиплікативними оберненнями підблоків ключа вжитого для шифрування. Для алгоритму IDEA прийнято, що мультиплікативна зворотність нуля є нуль.

Граф процесу дешифрування той самий, що і для процесу шифрування, єдина відмінність в тому, що підблоки ключа дешифрування K_i^(r) обраховуються з підблоків ключа шифрування Z_і^(r) наступним чином:

де Z^-1 визначено як інверсія множення (по модулю 2¹⁶+1) від Z, тобто ZZ^-1=1;

-Z визначено як інверсія додавання (по модулю 2¹⁶) від Z, тобто -Z[+]Z=0;

Обрахунок підблоків ключа дешифрування з підблоків ключа шифровання показаний в таблиці 1.

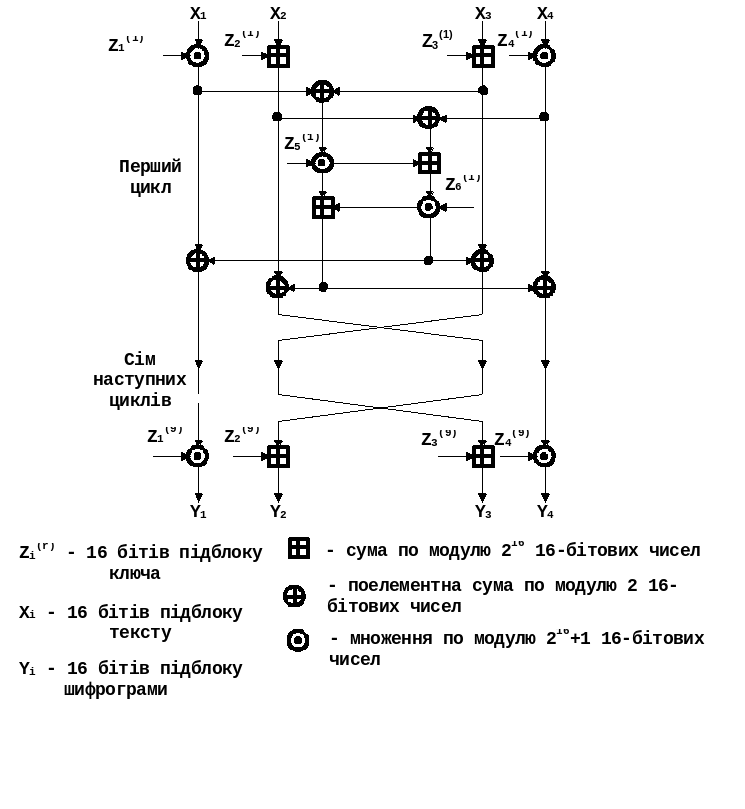Рис.4. Структурна схема алгоритму IDEA.

2.2.3.Розподіл ключів.

52 підблоки ключа довжиною 16 біт, що використовуються в процесі шифрування генеруються з 128-бітового ключа користувача наступним чином: 128-бітний ключ користувача поділяється на вісім підблоків, які безпосередньо використані в якості перших восьми підблоків ключа, де впорядковані підблоки ключа визначені як:

.

128-бітний ключ користувача потім циклічно зсувається вліво на 25 позицій, після якого результуючий 128-бітний блок знову поділяється на вісім підблоків, які взяті як наступні вісім підблоків ключа. Отриманий 128-бітний блок знову циклічно зсувається на 25 позицій вліво, щоб утворити наступні вісім підблоків ключа, і ця процедура повторюється поки всі 52 підблоки ключа не будуть згенеровані.

Таблиця №1

Цикл	Підблоки ключа шифрування	Підблоки ключа дешифрування
1
2
3
4
5
6
7
8
Кінцева перестановка

2.2.4.Групові операції і їх взаємозв`язок.

Шифр IDEA базується на новому понятті розробки змішаних операцій інших алгебраїчних груп однакової кількості елементів. Групові операції вибрані поскільки статистичне відношення трьох будь-яких змінних U; V; W зв`язане груповою операцією W=U*V має властивість "абсолютна секретність", якщо будь-яка з трьох випадкових змінних вибрана незалежно від інших і рівноймовірно і є любим груповим елементом, то дві інші випадкові змінні статистично незалежні. Взаємодія інших групових операцій забезпечує "путаницю" необхідну для безпечного шифру, пояснюється в двох наступних пунктах.

2.2.5.Характерестики безпеки idea.

Один із принципів створення IDEA - ускладнити диференційний криптоаналіз. Також не одна лінійна криптоаналітична атака не закінчилась успішно, як і не було виявлено алгебраїчно слабких місць.

Довжина ключа в алгоритмі IDEA становить 128 бітів - це понад в два рази більше ніж алгоритм DES. Така довжина ключа зумовлює те, що існує 2¹²⁸ (10³⁸) шифрограм. Якщо б спроектувати цифровий пристрій, який тестує міліард ключів в секунду і використати міліард таких пристроїв, то тривалість розпізнавання становила 10¹³ років, що набагато більше за час існування всесвіту. Мережа з 10²⁴ машин знайшла ключ на протязі дня, але в цілому всесвіті не знайшлося б стільки атомів кремнію, щоб побудувати стільки машин.

Самий повний аналіз провів Daemen. Він відкривив великий клас 2⁵¹ слабких ключів, при використанні яких в процесі шифрування, ключ може бути виявлений і відновлений. Однак, в IDEA існує 2¹²⁸ можливих варіантів ключів, то це відкриття не впливає на практичну безпеку шифру.

Щодо ключів, що є слабкими, то конкретне рішення по їх викоританню чи невикористанню залежить від розробника криптосистеми. З одної сторони, ймовірність появи саме слабкого ключа є практично нульовою, а з іншої не складним є перед використанням перевіряти ключі на їх належність до множини слабких, напівслабких чи частково слабких ключів.

Крім того, певну небезпеку з точки зору криптостійкості системи становить властивість комплементарності ключів. Комплементарні ключі - це ключі, протилежні за формою один одному - кожній одиничці одного ключа відповідає нолик в другому і навпаки.

Небезпека є в тому, що комплементарні ключі шифрують комплементарні тексти явні до комплементарних шифрограм. В результаті, при застосуванні атаки за допомогою тексту явного достатньо реалізувати лише половину переборів ключів від максимального числа 2¹²⁸. Біхам і Шамір показали, що при застосуванні такого методу потрібно як мінімум 2⁵¹ різних текстів явних. Слід сказати, що ефект від властивості комплементарності дуже легко зменшити, застосувавши перетворення вихідного тексту явного в послідовність більш-менш рівноймовірних символів, і тоді час, потрачений на аналіз комплементарних текстів в порівнянні з часом, затраченим на пробу ключа, зведе до нуля ефект комплементарності.

З початку впровадження IDEA точиться дискусія щодо криптостійкості, яка забезпечується таким ключем. І що цікаво, з плином часу оцінки експертів щодо необхідних затрат ресурсів часу і грошей для злому алгоритму, що має саме таку довжину ключа збільшуються.

В результаті цього до даного часу не доказано математично, за скільки ж часу можна все-таки ефективно перебрати 2¹²⁸ ключів.

Крім того, після впровадження в 1990 році Біхамом і Шаміром різнецевої атаки, питання про довжину ключа втратило актуальність через те, що для цього методу атаки на криптографічні системи довжина ключа не грає принципової ролі.

В зв”язку з цим єдиним критерієм можна назвати той, що довжина ключа повинна забезпечувати таку кількість комбінацій, яку не можна було б перебрати швидше того часу, за який можна реалізувати різнецеву криптоатаку.

В цьому розділі, вказано деякі доказані характеристики безпеки шифру IDEA.

Путаниця. Путаниця необхідна для безпечного шифру, в алгоритмі IDEA досягається змішуванням трьох несумісних групових операцій. В процесі шифрування для IDEA три групові операції так розмішуються, що вихідна операція одного типу ніколи не використана в якості вхідної операції того ж типу.

Три операції несумісні по змісту:

1. Ніяка пара трьох операцій не задовільняє "дистрибутивний" закон. Наприклад,для операцій  і [+], для a,b,c в F₂¹⁶:

1. a[+](bc)(a[+]b)(a[+]c).

1. Для прикладу,a=b=c=1=(0,0,...,0,1), ліва сторона нерівності 2=(0,0,...,0,1,0), права сторона - 4=(0,0,...,0,1,0,0).

1. Ніяка пара трьох операцій не задовільняє "узагальнений асоціативний" закон. Наприклад,для операцій [+] і , для a,b,c в F₂¹⁶:

1. a[+](bc)(a[+]b)  c.

1. Для прикладу,a=b=c=1=(0,0,...,0,1), ліва сторона нерівності 1=(0,0,...,0,1), права сторона - 3=(0,0,...,0,1,1). Таким чином не можна випадково змінити порядок операцій, щоб спростити аналіз.

1. Три операції зв`язуються прямим розподілом та інверсією. Шифрувальне значення в тому, що якщо б існував ізотопізм між двома операціями, тоді можна було одну операцію іншою прикладаючи взаємно-нежалежний розподіл на вході і виході.

Розсіювання. Перевірка прямих обчислень показала, що функція циклу - "завершена",тобто кожен вихідний біт першого циклу залежить від кожного біту відкритого тексту і від кожного біта ключа використаного на цьому циклі. Це рлзсіювання проводиться в шифрі IDEA перетворенням, що називається структура множення-додавання (МД), яка показана на рис.5. Структура МД перетворює два 16 бітні підблоки в два 16-ти бітні підблоки керовані двома 16-ти бітними підблоками ключа.

Рис.6. Граф МД структури

Ця структура має наступні особливості:

• для любого вибору підблоків ключа Z₅ і Z₆, МА(.,.,Z₅,Z₆) - зворотнє перетворення; для любого вибору U₁ і U₂, МА(.,.,U₁,U₂) - також зворотнє перетворення;

• ця структура має "завершене розсіювання" ефект якого полягає в наступному: кожен вихідний підблок залежить від кожного вхідного підблоку, і ця структура використовує найменшу кількість потрібних операцій (чотири), щоб досягнути такого повного розсіювання.