
- •1. Роль физики в познании мира
- •2. Понятие о физической картине мира (фкм)
- •3. Физика как система научных физических теорий
- •Механика
- •Термодинамика и молекулярная физика
- •Уравнение Ван-дер-Ваальса
- •Теплоемкость газов. Уравнение Майера
- •Адиабатический процесс
- •3. Молекулярные представления о диффузии, вязкости, теплопроводимости
- •Характеристики процессов переноса для жидкостей
- •4. Испарение и кипение жидкостей. Влажность воздуха и её измерение
- •Электричество и магнетизм
- •Движение заряженной частицы в магнитном поле
- •Сравнение полей
- •Ф арадей Максвелл
- •Квантовая физика Элементы физики атома и ядра
- •Люминесценция полярных сияний
Термодинамика и молекулярная физика
1. Термодинамическая система. Идеальный и реальный газы.
2. Вертикальный профиль температуры и давления в атмосфере Земли. Барометрическая формула.
3. Молекулярные представления о диффузии, вязкости, теплопроводимости.
4. Влажность воздуха и её измерение. Механизмы работы гейзеров.
5. Теория теплообмена. КПД тепловой машины. Атмосфера как гигантская тепловая машина. Облака и осадки. Циклоны, антициклоны, ураганы, торнадо. Общая циркуляция атмосферы.
1. Термодинамическая система. Идеальный и реальный газы
Внутренняя энергия, теплота, работа. Первый закон термодинамики. Идеальный газ как термодинамическая система. Уравнение Клапейрона-Менделеева.
![]() – основное уравнение
МКТ идеального газа.
– основное уравнение
МКТ идеального газа.
-
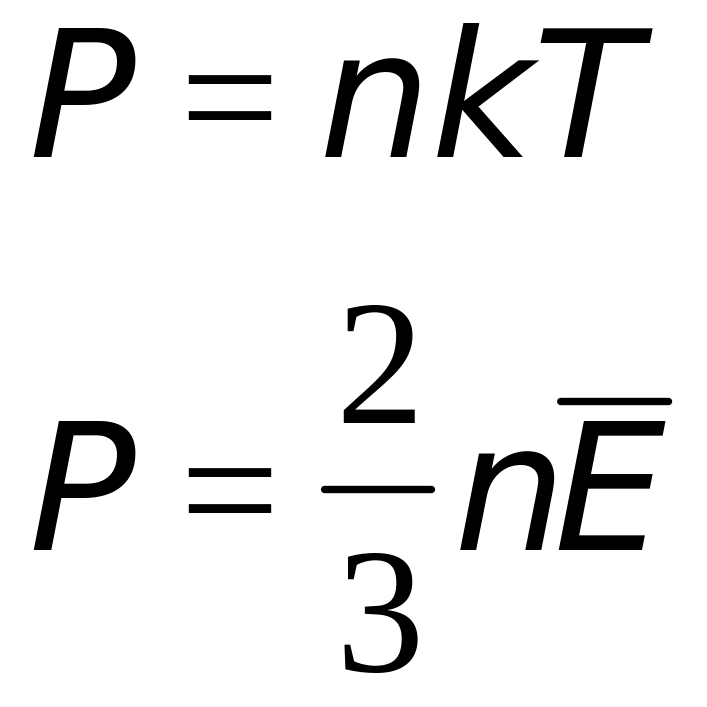
Р


![]()
P T
![]() ;
k = 1,38·10–23 Дж·К – 1
.
;
k = 1,38·10–23 Дж·К – 1
.
![]() – уравнение Клаузиуса.
– уравнение Клаузиуса.
Т = t˚+ 273 (К) – абсолютная температура (по шкале Кельвина).
Р = nkT – по существу данная формула уже есть уравнение состояния идеального газа.


![]() – уравнение
Менделеева (1874 г.)
– уравнение
Менделеева (1874 г.)
Установим связь параметров в двух разных состояниях газа: (m = const, M = const).
а )
P1, V1,
T1
б) P2, V2,
T2
)
P1, V1,
T1
б) P2, V2,
T2
![]()
![]()
![]() – Уравнение
Клапейрона (1834 г.) французский
физик.
– Уравнение
Клапейрона (1834 г.) французский
физик.
Уравнение Ван-дер-Ваальса
Модель идеального газа (когда взаимодействием молекул пренебрегают) достаточно хорошо описывает поведение реальных газов при условиях, близких к нормальным (0˚С и 105 Па). Однако при высоких давлениях и температурах, близких к абсолютному нулю, расстояния между молекулами настолько уменьшаются, что становится необходимым учитывать размеры молекул и их взаимодействие друг с другом. Так, при давлении воздуха в 1000 атмосфер объем молекул составляет уже половину объема газа, поэтому пренебрегать им нельзя.
Голландский
физик Ван-дер-Ваальс в 1873 году предложил
ввести в уравнение Клапейрона-Менделеева
(уравнение состояния идеального газа)
поправки: р´–
внутренне давление газа, обусловленное
взаимным притяжением его молекул, и b
– объем, занимаемый самими молекулами.
Тогда уравнение для 1 моля газа будет
выглядеть так: (p + p´)·(V – b) = RT,
здесь p´=![]() – коэффициент, зависящий от природы
газа.
– коэффициент, зависящий от природы
газа.
Тогда для произвольного количества реального газа уравнение состояния имеет вид:
![]() – уравнение
Ван-дер-Ваальса
– уравнение
Ван-дер-Ваальса
или
проще:
![]() .
Уравнение является весьма приближенным,
как впрочем, большинство физических
законов, кроме законов сохранения
электрического заряда, энергии, импульса
и момента импульса.
.
Уравнение является весьма приближенным,
как впрочем, большинство физических
законов, кроме законов сохранения
электрического заряда, энергии, импульса
и момента импульса.
У равнение
Ван-дер-Ваальса является кубическим
относительно объема, поэтому оно имеет
три корня для V,
т. е. данному
значению давления р
при Т= const
соответствуют
три значения объема (см. рис. 1) V.
В зависимости
от величины Т эти корни могут быть либо
все действительные и различные (тогда
кривая р(V)
имеет изгиб), либо два являются мнимыми
(не соответствуют реальным состояниям
системы) и только один действительным
(тогда кривая р(V)
монотонна). Изотерма, соответствующая
наивысшей температуре, при которой
уравнение Ван-дер-Ваальса имеет три
действительных значения корня для V,
называется
критической, а эта температура –
критической температурой.
равнение
Ван-дер-Ваальса является кубическим
относительно объема, поэтому оно имеет
три корня для V,
т. е. данному
значению давления р
при Т= const
соответствуют
три значения объема (см. рис. 1) V.
В зависимости
от величины Т эти корни могут быть либо
все действительные и различные (тогда
кривая р(V)
имеет изгиб), либо два являются мнимыми
(не соответствуют реальным состояниям
системы) и только один действительным
(тогда кривая р(V)
монотонна). Изотерма, соответствующая
наивысшей температуре, при которой
уравнение Ван-дер-Ваальса имеет три
действительных значения корня для V,
называется
критической, а эта температура –
критической температурой.
Р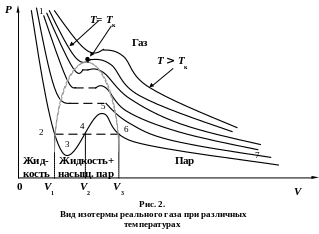 ассмотрим
более подробно изотерму, изображенную
на рис. 1. В этом случае все три корня
уравнения Ван-дер-Ваальса – действительные:
V1= Vmin
–
соответствует
жидкому состоянию вещества, V3= Vmax
–
соответствует
газообразному состоянию, V2
–
соответствует
динамическому равновесию между жидкостью
и паром данного вещества. На участках
1-3 и 5-7 с уменьшением объема давление
растет, что естественно. На участке 3-5
сжатие вещества приводит к уменьшению
давления, такие процессы в природе не
осуществляются. Наличие участка 3-5
означает, что при постепенном изменении
объема вещество не может оставаться
всё время в виде однородной среды; в
некоторый момент должно наступить
скачкообразное изменение состояния и
распад вещества на две фазы (на два
агрегатных состояния). Участок 2-3
соответствует состоянию перегретой
жидкости, а участок 5-6 – пересыщенному
пару. Истинная (реальная) изотерма имеет
вид ломаной линии 7-6-2-1. участок 6-7
соответствует газообразному состоянию,
а участок 2-1 – жидкому. В состояниях,
соответствующих горизонтальному участку
6-2, наблюдается равновесие жидкой и
газообразной фаз вещества. Вещество в
газообразном состоянии, при Т < Тк,
называется
паром, а пар,
находящийся в динамическом равновесии
со своей жидкостью, есть
насыщенный пар.
ассмотрим
более подробно изотерму, изображенную
на рис. 1. В этом случае все три корня
уравнения Ван-дер-Ваальса – действительные:
V1= Vmin
–
соответствует
жидкому состоянию вещества, V3= Vmax
–
соответствует
газообразному состоянию, V2
–
соответствует
динамическому равновесию между жидкостью
и паром данного вещества. На участках
1-3 и 5-7 с уменьшением объема давление
растет, что естественно. На участке 3-5
сжатие вещества приводит к уменьшению
давления, такие процессы в природе не
осуществляются. Наличие участка 3-5
означает, что при постепенном изменении
объема вещество не может оставаться
всё время в виде однородной среды; в
некоторый момент должно наступить
скачкообразное изменение состояния и
распад вещества на две фазы (на два
агрегатных состояния). Участок 2-3
соответствует состоянию перегретой
жидкости, а участок 5-6 – пересыщенному
пару. Истинная (реальная) изотерма имеет
вид ломаной линии 7-6-2-1. участок 6-7
соответствует газообразному состоянию,
а участок 2-1 – жидкому. В состояниях,
соответствующих горизонтальному участку
6-2, наблюдается равновесие жидкой и
газообразной фаз вещества. Вещество в
газообразном состоянии, при Т < Тк,
называется
паром, а пар,
находящийся в динамическом равновесии
со своей жидкостью, есть
насыщенный пар.
Если через крайние точки горизонтальных участков семейства изотерм (соответствующих различным температурам Т < Тк) провести линию, то получится колоколообразная кривая (см. рис. 2), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму состояний на четыре области: под кривой располагается область двухфазных состояний (жидкость + насыщенный пар), слева от неё, при Т < Тк, находится область жидкого состояния, а справа – область пара. Пар отличается от газа тем, что при изотермическом сжатии он превращается в жидкость. При Т > Тк, вещество может существовать только в газообразном состоянии, т. е. при Т > Тк вещество не может быть превращено в жидкость ни при каких давлениях. Иными словами, пар – это газ, находящийся при температуре, ниже критической. Отметим, что при критической температуре плотность и вязкость жидкости и газа одинаковы. Для воды Тк составляет 674 К = 374,15˚С, кислорода – 304 К, водорода – 13,2 К. Поэтому газообразная вода в атмосфере – это пар, так как Т < Тк, а кислород и азот в атмосфере – газы, так как их критические температуры (– 129˚С у кислорода и – 147˚С у азота) много ниже температуры атмосферы. Углекислота СО2 при Т > 31,1˚С – газ, а при Т < 31,1˚С – пар.
