ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

1.

3. Необходимое условие сходимости ряда:

Для сходимости ряда   необходимо, чтобы последовательность   была бесконечно малой.

Доказатетьство

По условию последовательность  , а следовательно, и её остаток   имеют общий конечный предел  , но   и поэтому  , что равносильно бесконечной малости  .

4. Геометри́ческая прогре́ссия — последовательность чисел   (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число   (знаменатель прогрессии), где  ,  : 

Любой член геометрической прогрессии может быть вычислен по формуле:

Если   и  , прогрессия является возрастающей последовательностью, если  , — убывающей последовательностью, а при   —знакочередующейся^[2].

Своё название прогрессия получила по своему характеристическому свойству:

то есть каждый член равен среднему геометрическому его соседей.

5. признаки сравнения рядов

Даны два ряда   и   − такие, что   для всех n. Тогда справедливы следующие признаки:

 Если   сходится, то   также сходится;

 Если   расходится, то   также расходится.

Предельные признаки сравнения рядов

Пусть даны два ряда   и  , у которых члены a_n и b_n положительны для всех n. Тогда справедливы следующие предельные признаки:

• Если  , то оба ряда   и   либо сходятся, либо расходятся;

• Если 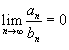 , то ряд   сходится, если сходится ряд  ;

• Если  , то ряд   расходится, если расходится ряд  .

Так называемый обобщенный гармонический ряд   сходится при p > 1 и расходится при 0 < p ≤ 1. 

Определить, сходится или расходится ряд  .

Решение.

Воспользуемся признаком сравнения. Заметим, что   для всех натуральных n. Ряд  является обобщенным гармоническим рядом с p = 2 > 1 и, следовательно, сходится.  Таким образом, исходный ряд сходится по признаку сравнения. 

6. Интегральный признак сходимости

Пусть функция  f(x)  непрерывна, положительна и не возрастает при x ≥ N ( N ≥ 1 - натуральное число). Ряд    с членами u_n = f (n) сходится или расходится одновременно с несобственным интегралом  . 

11. Сходящийся ряд   называется сходящимся абсолютно, если сходится ряд из модулей  , иначе — сходящимся условно.

Аналогично, если несобственный интеграл   от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля  .

Признаки абсолютной сходимости\

Признак сравнения

Если   при  , то:

• если ряд 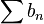  сходится, то ряд   сходится абсолютно

• если ряд   расходится, то ряд   расходится

Согласно критерию Коши,  . Значит,  , и по критерию Коши ряд   сходится. Второе утверждение следует из первого, так как если бы ряд   сходился, то и ряд   сходился бы.

12.

13. Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция  .

Сходимость

Ряд называется сходящимся поточечно, если последовательность   его частичных сумм сходится поточечно.

Ряд называется сходящимся равномерно, если последовательность   его частичных сумм сходится равномерно.

Необходимое условие равномерной сходимости

 при 

Или, что эквивалентно   , где Х - область сходимости.

Критерий Коши равномерной сходимости

Критерий Коши для функциональной последовательности. Чтобы последовательность функций  , определённых на множестве  , равномерно сходилась на этом множестве, необходимо и достаточно, чтобы для всякого  , начиная с некоторого номера  , при всех  , больше либо равных  , одновременно для всех   значения функций   и   различались не более, чем на  .

Абсолютная и условная сходимость

Ряд   называется абсолютно сходящимся, если   сходится. Абсолютно сходящийся ряд сходится.

Если ряд   сходится, а   расходится, то ряд   называется сходящимся условно. Для таких рядов верна теорема Римана о перестановке членов условно сходящегося ряда.

Признаки равномерной сходимости

Признак сравнения

Ряд   сходится абсолютно и равномерно, если выполнены условия:

1. Ряд 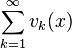  сходится равномерно.

2. 

Частным случаем является признак Вейерштрасса, когда  . Таким образом, функциональный ряд ограничивается обычным. От него требуется обычная сходимость.

Признак Дирихле

Ряд   сходится равномерно, если выполнены следующие условия:

1. Последовательность действительнозначных функций 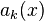  монотонна  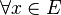 и 

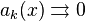
2. Частичные суммы 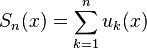  равномерно ограничены.

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ часть 2

1. Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда)

2. Числовой ряд – это сумма членов числовой последовательности вида  .

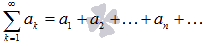В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5:  .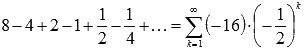

 называют общим членом числового ряда или k–ым членом ряда.

2.

Исследуем сходимость ряда

, (6)

 

который называется рядом геометрической прогрессии. Ряд (6) часто используется при исследовании рядов на сходимость.

Как известно, сумма первых n членов прогрессии находится по формуле  Найдем предел этой суммы

 

Рассмотрим следующие случаи в зависимости от величины q:

1. Если  , то  . Поэтому  ряд (6) сходится, его сумма равна  ;

2. Если  , то  . Поэтому  ряд (6) расходится;

3. Если  , то при  ряд (6) принимает вид  для него  и  т. е. ряд (6) расходится; при  ряд (6) принимает вид  – в этом случае  при четном n и  при нечетном n. Следовательно,  не существует, ряд (6) расходится.

Итак, ряд геометрической прогрессии сходится при  и расходится при  .

Пример 1. Показать, что ряд  сходится.

Решение: Данный ряд можно переписать так:

 

 

Как видно, он представляет собой ряд геометрической прогрессии с  и  . Этот ряд сходится согласно свойству 1 числовых рядов.