1. Глава 3. Электромеханические свойства двигателей переменного тока

Машины переменного тока имеют существенное преимущество перед коллекторными двигателями постоянного тока – они могут быть выполнены бесконтактными, что обеспечивает больший ресурс, высокую надежность и безопасность. Двигатели переменного тока находят применение, как в управляемых, так и в неуправляемых приводах. В настоящей главе мы рассмотрим характеристики наиболее распространенных машин переменного тока асинхронных и синхронных.

1. 3.1. Электромеханические свойства асинхронных двигателей

Назначение асинхронного двигателя в наибольшей степени определяет его конструкцию. В общепромышленных неуправляемых приводах малой и средней мощности используются двигатели с короткозамкнутым ротором. В более мощных приводах, и там где требуется ограничение пусковых токов, применяют двигатели с фазным ротором. Приборную автоматику обслуживают приводы на малоинерционных управляемых асинхронных двигателях. В последнее время, в связи с развитием различных вариантов частотного управления, во всех типах управляемых приводов находят применение асинхронные двигатели с короткозамкнутым ротором. Поэтому наибольшее внимание уделим классическим трехфазным двигателям с короткозамкнутым и с фазным ротором.

1. 3.1.1. Математическое описание процессов преобразования энергии в асинхронных машинах

Математическое описание электромагнитных процессов в машинах переменного тока намного сложнее, чем в машинах постоянного тока. Это объясняется не только тем, что их питание осуществляется переменным током, но и тем, что в таких машинах имеются несколько взаимосвязанных электрических контуров. В результате при описании электромагнитных процессов мы получаем систему дифференциальных уравнений высокого порядка. В теории электромеханического преобразования энергии существуют различные методы упрощения исходных уравнений. Наиболее распространенным из них является представление электрической машины в виде идеализированного двухфазного электромеханического преобразователя. В идеализированной машине в воздушном зазоре имеем круговое поле, а высшие гармоники отсутствуют. Методы перехода от исходной трехфазной машины к идеализированной хорошо разработаны в общей теории электромеханического преобразования энергии – на них останавливаться не будем. Отметим лишь, что в результате преобразований мы получим идеализированную машину, имеющую две обмотки на роторе и две обмотки на статоре, расположенные по ортогональным осям α и β (рис. 3.1). Для такой машины справедлива система уравнений:

(3.1)

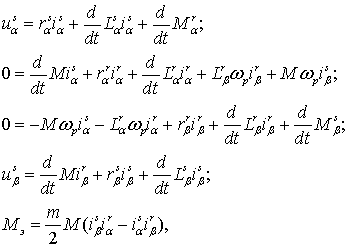
где u_α^s,u_β^s – напряжения на обмотках статора; i_α^s,i_α^r,i_β^s,i_β^r – токи в обмотках статора и ротора по осям α и β; L_α^s,L_α^r,L_β^s,L_β^r – полные индуктивности обмоток статора и ротора по осям α и β; m – число фаз двигателя; M_э – электромагнитный момент двигателя.

Рис. 3.1. Модель идеализированной асинхронной машины

Полная индуктивность каждой обмотки может быть записана уравнением

L=M+L_σ

где M – взаимная индуктивность между обмотками ротора и статора по осям α и β; L_σ – индуктивность рассеяния обмотки. Система уравнений (3.1) достаточно точно описывает статические и динамические процессы в асинхронном двигателе, если принят гармонический закон изменения напряжений u_α и u_β. Однако она является существенно нелинейной и в таком виде практически не используется. Для упрощения математического описания электромагнитных процессов осуществляют преобразования исходных уравнений. В частности, если в первых четырех уравнениях системы (3.1) провести замену d/dt↔jω, получим систему уравнений асинхронного двигателя в установившемся режиме:

(3.2)

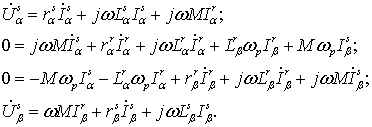
Так как рассматривается симметричная машина, целесообразно параметры обмоток обозначитьL_s=L_α^s=L_β^s, R_s=r_α^s=r_β^s, L_r=L_α^r=L_β^r, R_r=r_α^r=r_β^r, а также ввести понятия x_s=ωL_s,x_r=ωL_r – полные индуктивные сопротивления статора и ротора, x₀=ωM – сопротивление взаимной индукции. Кроме того, обозначим результирующие векторы напряжений   и токов  ,  . Тогда от четырех уравнений напряжений (3.2), если обратиться к обобщающим векторам напряжений, токов и сопротивлений, можно перейти к двум уравнениям:

(3.3)

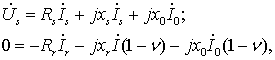
где ν=ω_р/ω. Введем понятия скольжение ротора относительно поля статора s=(ω−ω_р)/ω и ЭДС холостого хода  . Тогда систему уравнений асинхронной машины можно представить в виде:

(3.4)

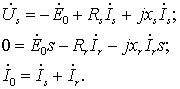
Обозначим z_s=R_s+jx_s, z_r=R_r+jx_r, разделим второе уравнение системы (3.4) на s и с учетом того, что R_r/s=R_r+R_r×(1−s)/s, получим

(3.5)

Полученные уравнения описывают электромагнитные процессы асинхронного двигателя в установившемся режиме. По ним строятся векторные диаграммы и схемы замещения двигателя. В частности, если перейти к приведенным параметрам роторной цепи, систему уравнений (3.5) можно представить в виде

(3.6)

Векторная диаграмма, соответствующая уравнениям (3.6) представлена на рис. 3.2.

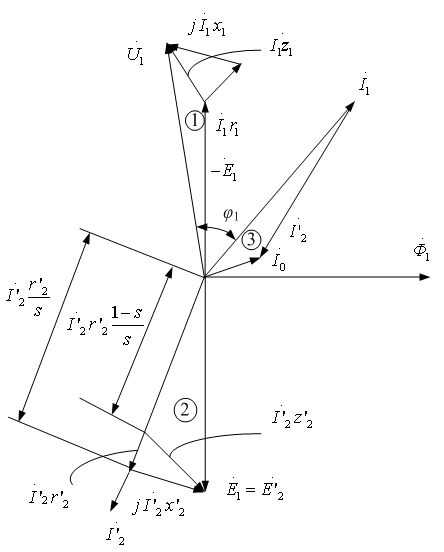
Рис. 3.2. Векторная диаграмма асинхронной машины