Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

“Рязанский государственный университет им. С.А.Есенина”

Задания к контрольным работам

по дисциплине

Дискретная математика

для специальности 030100.00; информатика и английский язык

факультет иностранных языков

курс 3 семестр 5

всего часов (включая самостоятельную работу) 90

для специальности 030100, информатика (заочное отделение)

факультет физико-математический

курс 4 семестр 7

всего часов (включая самостоятельную работу) 44

Задания составлены

канд. техн. наук, доцентом Н.В. Богдановой

канд. техн. наук, доцентом В.С. Богдановым

Рязань 2006

Пояснительная записка

Предложенные варианты заданий к контрольным работам могут использоваться как для специальности очного обучения, так и заочного. Для заочного обучения (специальность «Информатика») задачи разбиты по 10 вариантам и сгруппированы по основным темам курса с учетом часов учебного плана для данной дисциплины. Студентам предложено решить задачи и оформить отчет. В отчете необходимо привести основные положения теории, основные теоремы, формулы, на основе которых выполняется задание, а также подробный алгоритм решения.

Для специальности очного обучения («Информатика и английский язык») данные задачи можно использовать для срезовых контрольных работ, закрепляя пройденный материал.

0 Вариант

Теория множеств

Решить задачи и представить решения в виде кругов Эйлера.

1. Дано А = {е, л ,ь}

В = {д, р, е, в, о}

С = {д, р, о, в, а}

Найти: А U B ∩ C =

(A U C) \ (B U A) =

C \ (B ∩ A) =

2. Мощность Булеана N(B_С) =

Комбинаторика

1. В селении живут 1500 жителей. Доказать, что по крайней мере двое из них имеют одинаковые инициалы.

2. Всем участникам автопробега не повезло. 12 из них увязли в песке – пришлось толкать машину, 8 понадобилась замена колеса, у шестерых перегрелся мотор, пятеро толкали машину и меняли колесо, четверо толкали машину и остужали мотор, трое меняли колесо и остужали мотор. Одному пришлось испытать все виды неполадок. Сколько всего было участников автопробега?

3. Сколькими способами можно разделить m+n+s-предметов на 3 группы так, чтобы в одной группе было m предметов, в другой – n предметов, в третьей- s предметов?

4. Сколько существует способов размещения 60 пассажиров в 5 вагонах поезда при условии, что 2 вагона будут свободны?

5. На сколько частей делят плоскость 7 прямых, если никакие из 2х не параллельны и пересекаются в одной точке только по 2-е?

Графы

Даны графы G и R

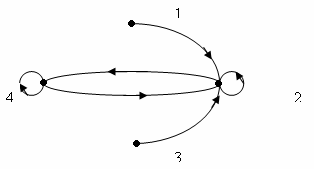
G R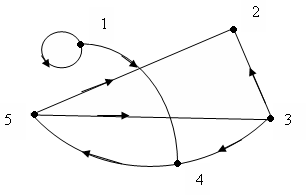

1. Построить матрицы смежности графов

2. Найти дополнение графов до полного

3. Найти:

   1. G ∩ R

б) G U R

Построить результирующие графы.