Теорема об оценках
Значения
переменных 
в
оптимальном решении двойственной задачи
представляют собой оценки влияния
свободных членов 
системы
ограничений – неравенств прямой задачи
на величину 
:
.
Диапазон
изменения компонент вектора 
,
в котором сохраняется оптимальный
базис, называется Областью устойчивости
оптимальных оценок.
Экономический
смысл первой теоремы двойственности
следующий. План производства 
и
набор ресурсов 
оказываются
оптимальными тогда и только тогда, когда
прибыль от реализации продукции,
определенная при известных заранее
ценах продукции 
,
равна затратам на ресурсы по «внутренним»
(определяемым только из решения задачи)
ценам ресурсов
.
Для всех других планов прибыль от
продукции всегда меньше или равна
стоимости затраченных ресурсов 
,
т. е. ценность выпущенной продукции не
превосходит суммарной оценки затраченных
ресурсов. Значит, величина 
характеризует
производственные потери в зависимости
от рассмотренной производственной
программы и выбранных оценок ресурсов.
Целочисленное программирование. Общая формулировка задачи.
Некоторые задачи линейного программирования требуют целочисленного решения. К ним относятся задачи по производству и распределению неделимой продукции (выпуск станков, телевизоров, автомобилей и т. д.). В общем виде математическая модель задачи целочисленного программирования имеет вид
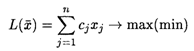
При ограничениях:
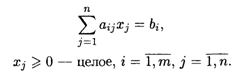
Оптимальное решение задачи, найденное симплексным методом, часто не является целочисленным. Его можно округлить до ближайших целых чисел. Однако такое округление может дать решение, не лучшее среди целочисленных решений, или привести к решению, не удовлетворяющему системе ограничений. Поэтому для нахождения целочисленного решения нужен особый алгоритм. Такой алгоритм предложен Гомори и состоит в следующем.
Симплексным методом находят оптимальное решение задачи. Если решение целочисленное, то задача решена. Если же оно содержит хотя бы одну дробную координату, то накладывают дополнительное ограничение по целочисленности и вычисления продолжают до получения нового решения. Если и оно является нецелочисленным, то вновь накладывают дополнительное ограничение по целочисленности. Вычисления продолжают до тех пор, пока не будет получено целочисленное решение или показано, что задача не имеет целочисленного решения.
Пусть
получено оптимальное решение 
Опт
= (F1, F2, ... , Fr, 0, ..., 0), которое не
является целочисленным, тогда последний
шаг симплексной таблицы имеет следующий
вид:
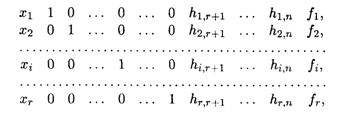
Где R — ранг системы ограничений; Hi,R+1 — коэффициент симплексной таблицы I-й строки, (R + 1)-го столбца; Fi— свободный член I-й строки.
Пусть Fi и
хотя бы одно Hij (J = 
,
r = 
)
— дробные числа.
Обозначим через [Fi] и [Hij] целые части чисел Fi и Hij.
Определение 1. Целой частью числа Fi называют наибольшее целое число, не превосходящее числа Fi.
Дробную часть чисел Fi и Hij обозначим {Fi} и {Hij}, она определяется следующим образом:
Общий вид задач нелинейного программирования.
В общем виде задача нелинейного программирования состоит в определении максимального (минимального) значения функции
(15.1)
при условии
(15.2)
где 
–
некоторые известные функции n переменных,
а 
–
заданные числа.
Класс
задач нелинейного программирования
шире класса задач линейного программирования.
Подробное изучение практических задач,
которые условились считать линейными,
показывает, что они в действительности
являются нелинейными. Существующие
методы позволяют решать узкий класс
задач, ограничения которых имеют вид 
,
а целевая функция
является сепарабельной (суммой n функций 
),
или квадратической.
Даже если область допустимых решений – выпуклая, то в ряде задач целевая функция может иметь несколько локальных экстремумов. С помощью большинства же вычислительных методов можно найти точку локального оптимума, но нельзя установить, является ли она точкой глобального (абсолютного) оптимума или нет. Если задача содержит нелинейные ограничения, то область допустимых решений не является выпуклой и кроме глобального оптимума могут существовать точки локального оптимума.