Решение систем m линейных неравенств с двумя переменными.
Дана система Т линейных неравенств с двумя переменными
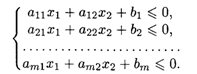
Знаки некоторых или всех неравенств могут быть ≥.
Рассмотрим первое неравенство в системе координат Х1ОХ2. Построим прямую
Которая является Граничной прямой.
Эта прямая делит плоскость на две полуплоскости 1 и 2 (рис. 19.4).
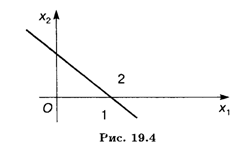
Полуплоскость 1 содержит начало координат, полуплоскость 2 не содержит начала координат.
Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произвольную точку на плоскости (лучше начало координат) и подставить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.
Направление полуплоскости на рисунках показываем стрелкой.
Определение 1. Решением каждого неравенства системы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.
Определение 2. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется Областью решения системы (ОР).
Определение 3. Область решения системы, удовлетворяющая условиям неотрицательности (Xj ≥ 0, J = ), называется Областью неотрицательных, или допустимых, решений (ОДР).
Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной областью или одной точкой.
Если система неравенств несовместна, то ОР и ОДР — пустое множество.
Симплекс-метод решения задачи линейного программирования. Выбор первоначального опорного плана. Улучшение опорного решения.
Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.
Основное содержание симплексного метода заключается в следующем:
Указать способ нахождения оптимального опорного решения
Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения
Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или следать заключение об отсутствии оптимального решения.
Алгоритм симплексного метода решения задач линейного программирования
Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее:
Привести задачу к каноническому виду
Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений)
Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода
Если выполняется признак единственности оптимального решения, то решение задачи заканчивается
Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения