18. Дифференциальное уравнение движения жидкости (уравнение движения Эйлера)
Для
решения задачи о движении невязкой
жидкости нужно составить уравнения
движения, связывающие между собой
скорости, давления и массовые силы,
действующие в жидкости.
Чтобы
получить эти уравнения, используем
векторное уравнение движения жидкости,
выраженное через напряжения
 .
.
В
невязкой жидкости действуют только
нормальные напряжения, связь которых
с давлениями имеет вид:
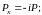

 .
.
Подставляя
эти значения в уравнение в напряжениях,
получим
уравнение:
 .
.
Или
используя понятие градиента скалярной
функции P
 (5.1)
(5.1)
Полученное
уравнение называется дифференциальным
уравнением
движения невязкой жидкости в форме
Эйлера.
Получим
уравнение в скалярной форме, спроецировав
его на оси координат:
 ;
;
 ;
(5.2)
;
(5.2)
 .
.


 .
.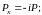

 .
. .
. (5.1)
(5.1) ;
; ;
(5.2)
;
(5.2) .
.