Факторный анализ (фа)

– группа методов, предназначенных для снижения размерности пространства переменных; для перехода от большего количества исходных переменных к значительно меньшему количеству новых переменных при условии сохранения большей части имеющейся информации.

Метод ФА отличается по идеологии.

Метод главных компонент (мгк)

Журнал: Социология 4М.

x₁ x₂ x₃ … x_k

y₁ y₂ y₃ … y_l

l << k (значительно меньше (в 2-3 раза)).

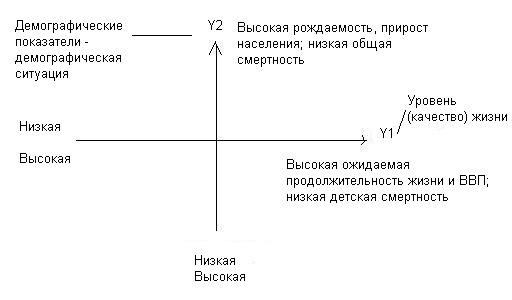
Подбор переменных можно представить в виде пространство, соответствующее их количеству; углы между ними зависят от силы корреляции. Если есть корреляция, угол острый.

I этап:

Свойства:

1) Всегда

2)

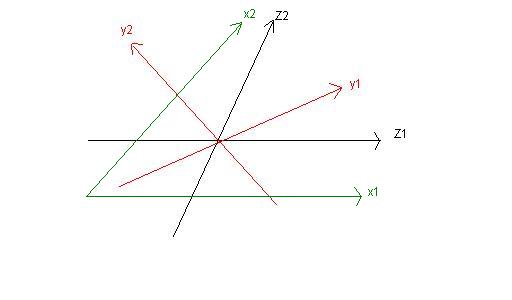
II этап: Ортогонизация пространства переменных:

Z_i ---> y_i

Требования:

Ортогональность yi: перпендикулярные углы

S2y1 > S2y2 > S2y3 > … > S2yl

диспозиции y заранее известны; значения матрицы корреляции; S2yi = λi; ∑λ = k

S²₁ + S²₂ + … + S²_k = k.

Результат I и II этапов: y_i = a_i1Z₁ + a_i2Z₂ + … + a_ikZ_k;

Общности – процент сохранённой информации переменной после выбора наиболее полезных переменных. Если % ≈ 10, то неудачное решение. Лучшее – если 80-90%.

III этап: Вращение для упрощения матрицы нагрузок – a_ij, исходная переменная x_i на главную компоненту y_i. Матрица нагрузок простая, если каждая исходная переменная имеет значительную по величине нагрузку только на один главный компонент. Меняется S2 главных компонент, но сумма не меняется; там, где высокая, понижается; там, где низкая, повышается.

IV этап: сокращение размерности пространства переменных, когда сокращаются данные с большими номерами.

V этап: Вращение главных компонент в пространстве исходных переменных с целью достижения простоты матрицы нагрузок.

Метод направлен на сохранение всех главных компонент, у которых S² = 1.

Классификация нескольких переменных

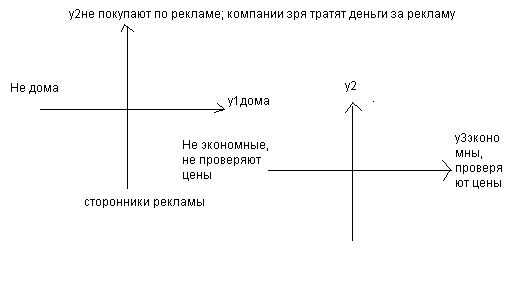
y₁ – домоседство

y₂ – недоверие к рекламе

y₃ – экономия

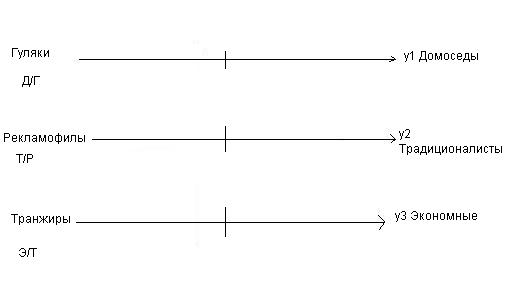
Типы потребительского поведения:

ДРЭ ГРЭ

ДРТ ГРТ

ДТЭ ГТЭ

ДТТ ГТТ

Иллюзия: респонденты в одной точке, но на самом деле они различаются по 3-м переменным.

Другие методы определения количества главных компонент

Необходимо выбирать метод в зависимости от того, что исследователь хочет получить; с точки зрения теории; гипотез; наблюдения и прочего.

2. Сохраняется определённый процент информации (например, 90%).

3. Автор – Кателл. Метод Кателла:

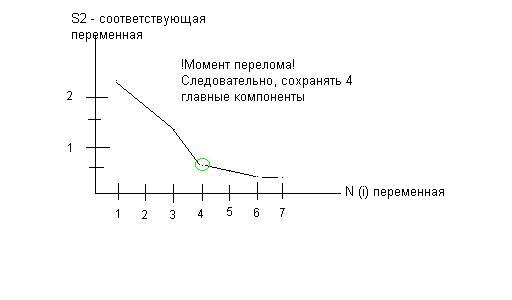
Интерпретация главных компонент. Подходы

1. Главные компоненты размера – применяется, когда все значительные по величине нагрузки на ГК имеют одинаковый знак. ГК интерпретируется как единственный показатель, упорядоченный респ. от полного его отсутствия до высокой степени присутствия.

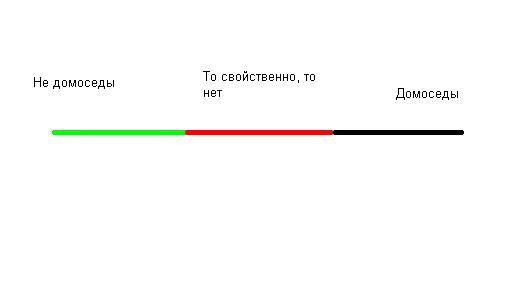
2. Главные компоненты формы – когда большие по размеру нагрузки имеют разные знаки. ГК интерпретируют как биполярная шкала, на противоположных концах которой находятся респонденты, с поведением, соответствующим 1 из 2 характеристик.

Графическое представление результата метода главных компонент: в пространстве главных компонент можно представить объекты – различия между респондентами и выявление их поведенченских типов.

I. 1) стоимость

2) тип подъёмника

3) глубина снега

4) качество

	Y1	Y2
1	-0,09	0,98
2	-0,07	-0,98
3	0,99	0,03
4	0,59	-0,04
	S2y1 = 2,00 (50%)	S2y2 = 1,92 (48%)

Y₁ = -0,09x1 - 0,07x2 + 0,99x3 + 0,59x4

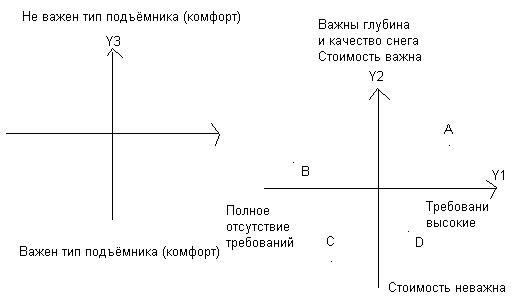
Недорого, снег:

y₁ > 0

y₂ > 0

Дорого, сердито:

y₁ > 0

y₂ < 0

Недорого, снег не обязателен:

y₁ < 0

y₂ > 0

Дорого, снег не обязателен:

y₁ < 0

y₂ > 0

II.

		Y1	Y2
x1	родной язык	0,55	0,43
x2	иностранный язык	0,57	0,29
x3	история	0,33	0,45
x4	арифметика	0,74	-0,27
x5	алгебра	0,72	-0,21
x6	геометрия	0,6	-0,13

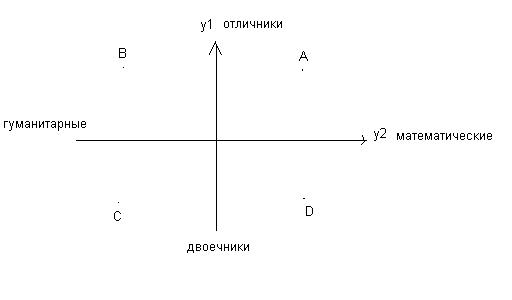
После вращения:

	Y1	Y2
x1	0,37	0,59
x2	0,43	0,47
x3	0,21	0,56
x4	0,79	0,00
x5	0,75	0,05
x6	0,6	0,08

Математические на Y2 не влияют.

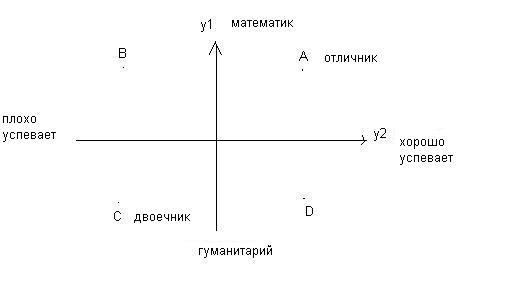
III.

	Component	Total	Cumulative %
1	4,073		58,190
2	1,820		84,195
3	0,451		90,638
4	0,359		95,764
5	0,159		98,038
6	.8Е-02 (=0,008)		99,190
7	.6Е-02 (=0,006)

SPSS сохраняет автоматически всё, что меньше 1, если не задать по % информации.