Корреляционный и регрессионный анализ

Коэффициент корреляции Пирсона.

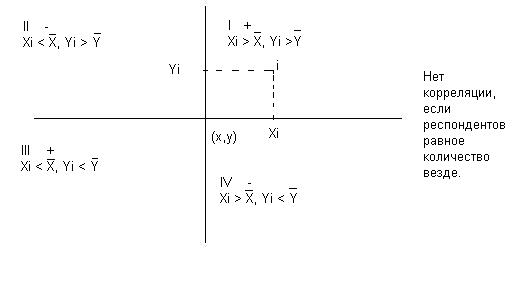
Матрица корреляции используется для изучения структуры связей между переменными и представляет собой квадратную таблицу, в которой на пересечении строк и столбцов указываются коэффициенты корреляции между соответствующей парой переменных.

n – объём выборки. К – количество одновременно анализируемых переменных. x1, x2.

x1 x2 … xj … xk

x1	1	r12
x2	r21	1
…			1
xi				1
…					1
xk						1

x₁ – оценка учебника студентами по 20-б шкале

x₂ – количество иллюстраций

x₃ – автор (1 – зарубежный, 0 – отечественный) - дихотомич

x₄ – кол-во страниц в книжке

x₅ – цена

	x1	x2	x3	x4	x5
x1	1	0,84	0,66	0,83	0,75
x2		1	0,77	0,71	0,76
x3			1	0,55	0,72
x4				1	0,76
x5					1

(3)

Первопричина – автор (традиции). Зависят иллюстрации, страницы; от них – цена, от всего этого – оценка студентов.

х1 – образование (в годах)

х2 – должность (1 – менеджер, 0 – все остальные)

х3 – стаж работы в фирме

х4 – зарплата

х5 – пол (1 – ж, 0 – м. Гипотеза: з/п женщин меньше)

	x1	x2	x3	x4	x5
x1	1
x2	0,51	1
x3	0,05	0,01	1
x4	0,66	0,73	0,2	1
x5	-0,36	-0,38	0,01	-0,48	1

(4)

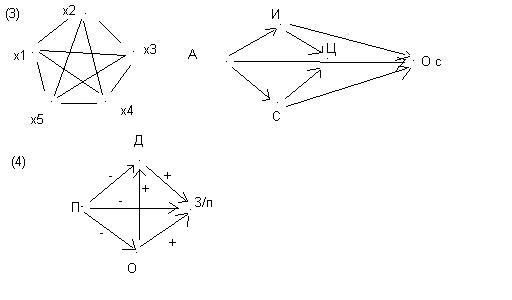
Выбор r_min: 1) сохранить как можно больше информации (все нельзя). Чем меньше коэффициент, тем больше информации мы сохраняем; 2) граф должен быть понятным и прозрачным: там должно быть меньше связей.

28.02.

1 – образование отца

2 – статус отца (в момент начала карьеры сына)

3 – образование сына

4 – статус сына (1: в начале трудовой карьеры)

5 – статус сына (2: на момент исследования)

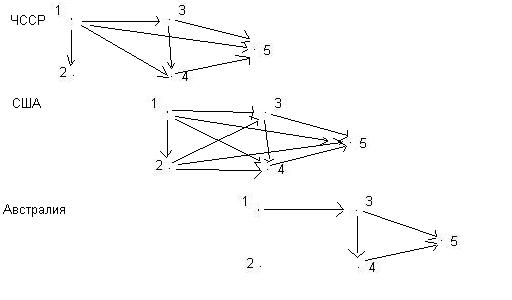
Страны: ЧССР; США; Австралия

Цель: в какой стране наиболее открытое общество (общество равных возможностей, независимо от того, кем являются родители).

ЧССР

	x1	x2	x3	x4	x5
x1	1	0,32	0,5	0,32	0,34
x2		1	0,18	0,22	0,18
x3			1	0,58	0,65
x4				1	0,54
x5					1

США

	x1	x2	x3	x4	x5
x1	1	0,52	0,45	0,33	0,32
x2		1	0,44	0,42	0,4
x3			1	0,54	0,65
x4				1	0,54
x5					1

Австралия

	x1	x2	x3	x4	x5
x1	1	0,29	0,47	0,24	0,23
x2		1	0,18	0,19	0,29
x3			1	0,43	0,43
x4				1	0,4
x5					1

1 – медианный возраст населения

2 – рождаемость

3 – смертность

4 – естественный прирост

5 – детская смертность

6 – ожидаемая продолжительность жизни М

7 – ожидаемая продолжительность жизни Ж

8 – ВВП

	1	2	3	4	5	6	7	8
1	1
2	-0,74	1
3	0,26	-0,46	1
4	-0,55	0,81	-0,9	1
5	-0,78	0,5	-0,04	0,5	1
6	0,39	-0,01	-0,75	0,38	-0,49	1
7	0,53	-0,08	-0,63	0,27	-0,63	0,92	1
8	0,39	0,08	-0,55	0,4	-0,58	0,77	0,83	1

Не факт, что правильный граф:

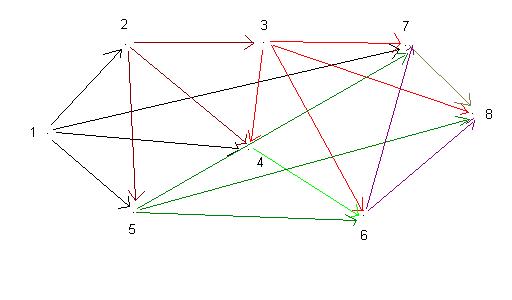
Регрессионные модели причинных связей

Принципы (Критерии) причинности (каузальности):

1) причина всегда предшествует следствию во времени (исключения: пол, возраст, среда выхода: место рождения, кто родители, образование, уровень доходов);

2) между причиной и следствием должна быть хотя бы корреляционная связь;

3) на взаимодействие причины и следствия не должны влиять третьи переменные. Проблема решается посредством включения в уравнение всех переменных, влияющих на связь между изучаемыми явлениями.

Если не выполняется хотя бы 1 принцип, то связь не причинна. Если все присутствуют, то это не значит, что связь причинна.

Модели влияния третьей переменной (1).

Задачи
объяснение изменений зависимой переменной от влияния независимых	прогнозирование (предсказание) значения зависимой переменной для объектов с определённым набором значений независимых переменных

Виды моделей:

1) уравнение множественной линейной регрессии

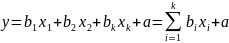
r² € (0;1)

1

X

Y

) r = 0

2) r ≠ 0

X

Y

r

Пример: r² = 0,2; r ≈ 0,45

Все различные значения переменной y на 20% зависит от x (а на 80% – от других факторов).

3

Y

)

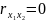
X₁

X₂

R² = r²yx₁ + r²yx₂ проблема мультиколлениарности; R – как 2 x относятся к y.

Y

4 ) r²x₁x₂ ≠0 r₁ 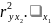- после устранения влияния Х₁

X₁

X₂

Мультиколлениарность – проблема: в регрессионном уравнении независимые переменные коррелируют между собой -> влияют на взаимодействие каждой из них на отношения с зависимой переменной.

Коэффициент детерминации r².

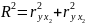(без учёта X₁)

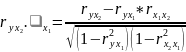
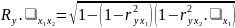
	X1 медианный возраст	X2 рождаемость	Y детская смертность
X1 медианный возраст	1	-0,74	-0,78
X2 рождаемость		1	0,5
Y детская смертность			1

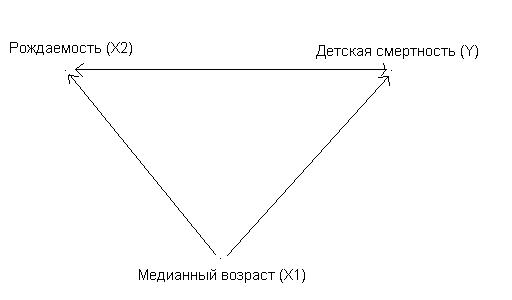
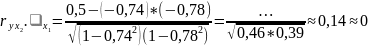
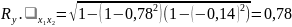
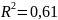
Коэффициент множественной корреляции всегда является положительным.

Детская смертность объясняется возрастом (на 60%) и рождаемостью.

На 60% детская смертность объясняется медианным возрастом и рождаемостью; роль рождаемости незначительна.

	Y – оценка	X1 – количество иллюстраций	X2 – количество страниц
Y – оценка	1	0,84	0,83
X1 – количество иллюстраций		1	0,71
X2 – количество страниц			1

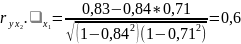
На 0,6² – 36% - зависит оценка от толщины книги.

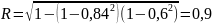
R = 0,81

Оценка зависит на 80% от количества иллюстраций и страниц, на 20% – от других факторов.

Оценка(y) = 0,12(b) иллюстраций(x) + 7,93(a).

b – насколько в среднем изменится у при изменении b на 1.

Если повысить иллюстрации на 1, то оценка изменится на 12 баллов.

Если иллюстрации = 0, то a (7,93): книги без иллюстраций имеют оценку 7,93 по 20-балльной шкале.

Если иллюстраций 50, то: 0,12 * 50 + 7,93 = 6 + 7,93 = 13,93 (баллов).

R₂ = 0,7 (1 модель).

Оценка = 0,07*илл + 0,01*стр + 5,59

y = b₁x₁ + b₂x₂ + a

0,07*100 + 0,01*200 + 5,59 = 7 + 2 + 5,59 = 14,59

R₂² = 0,87

Использование номинальных переменных в качестве независимых в уравнении регрессии

Дихотомические переменные (её можно сделать из любой переменной; их разрешено использовать в математических формулах).

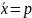(доля положительных ответов).

Всего респондентов = 10, "да" = 6, доля положительных ответов = 0,6.

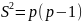
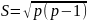
Пол: 1 – Ж 2 – М. Дихотомизирование: 1) 1 – Ж; 0 – М; 2) 1 – М; 0 – Ж.

З/п = 3400*обр – 8300*female – 8200

y = b₁ x₁ b₂ x₂ a

b₁ = каждый дополнительный год образования даёт к з/п 3400$ США.

b₂ = Ж по сравнению с М в среднем зарабатывают меньше на 8300.

x₂ = то, что под № 1.

З/п(м) = 3400*16 – 8200 = 46200.

Для М с бакалаврским образованием з/п составляет 46200.

З/п(ж) = 3400*16 – 8300 – 8200 = 37900.

Для Ж с бакалаврским образованием з/п составляет 37900.

Оценка = 4,24*з.авт. + 9,67

В среднем зарубежные книги оцениваются на 4,24 балла выше, чем отечественные

R² = 44% (0,44).

Автор определяет оценку книге на 44%.

Оценка = 0,21*авт + 0,12*илл + 7,94

R² = 0,7. Совпадает с первым примером: привнесение автора ничего не изменило.

Корреляция между оценкой и автором ложная.