8.4. Реакции опор для расчета подшипников

Так как направление вектора консольной силы от действия муфты предусмотреть невозможно, то в дальнейших расчетах направления векторов реакций опор от консольной силы условно принимаем совпадающими с направлениями векторов реакций от сил в зацеплении.

Таким образом, максимальные значения реакций в опорах определяем как арифметическую сумму реакций от сил в зацеплении и реакций от консольной силы, Н:

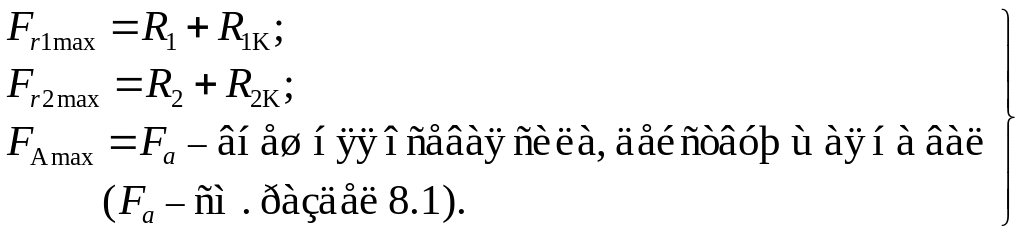(8.20)

Для подшипников, работающих при типовых режимах нагружения, расчеты удобно вести с помощью коэффициента эквивалентности . При этом по известным максимальным длительно действующим силам находим эквивалентные нагрузки, Н:

; ; (8.21)

где 0,56 – коэффициент эквивалентности для типового режима III [см. 1, стр. 116].

В соответствии с разработанной конструктивной схемой редуктора (см. конструктивную схему №2) подшипник опоры 2 на один типоразмер больше подшипника опоры 1. Это решение принято в связи с тем, что осевая сила косозубой зубчатой передачи направлена в сторону опоры 2. В результате подшипник опоры 2 кроме радиальной нагрузки воспринимает еще и осевую нагрузку, т.е. =0, = .

Для прямозубой зубчатой передачи осевая нагрузка на подшипники отсутствует, поэтому =0 и =0.

Определяем эквивалентную динамическую радиальную нагрузку на подшипники опор 2 и 1 по общей зависимости в виде,H:

, (8.22)

где −коэффициент вращения кольца подшипника: =1 при вращении внутреннего кольца;

−коэффициент динамичности нагрузки [см. 1, таблица 7.6]. Для принятых в разделе 8.1 условий работы принимаем =1,4;

−температурный коэффициент: =1 при (см. раздел 8.1).

и −коэффициенты радиальной и осевой нагрузок. Для определения и рассматриваем отношение по сравнению с коэффициентом осевого нагружения :

а) если (здесь =0,68 для радиально-упорных шарикоподшипников с углом контакта =26°), то принимаем =0,41 и =0,87[см. 1, таблица 7.2];

б) если , то принимаем =1 и =0.[см. 1, примечание к таблице 7.2].

Примечание. Для радиально-упорных шарикоподшипников с углом контакта коэффициент осевого нагружения определяется по формуле: , где – коэффициент, зависящий от геометрии деталей подшипника. находят по таблице 7.3 [1] в зависимости от отношения , где – диаметр шарика, – средний диаметр подшипника ( и – см. данные шарикоподшипника в разделе 7.2 для левой опоры); – статическая радиальная грузоподъемность подшипника (там же); – осевая сила в зубчатом зацеплении (см. раздел 8.1). Коэффициенты и в этом случае определяются следующим образом: