Период квантования импульсной сар, теорема Котельникова
Если непрерывную зависимость в результате квантования заменили решетчатой функцией, происходит потеря части информации. Такая потеря информации происходит и в результате работы импульсных модуляторов. В пределе, при бесконечной частоте квантования, получается непрерывный сигнал. Представляет интерес нижний предел частоты квантования. В самом деле, если частота низка, непрерывный сигнал за один интервал может весьма существенно измениться. Следовательно, может оказаться невозможным восстановление исходного сигнала по его решетчатой функции [1].
Особенностью импульсной САУ является то, что частотные характеристики представляют собой периодические функции частоты w0.
/T
Периодичность
частотных характеристик импульсной
САУ, а также их симметричность относительно
оси ординат, означает, что для их полного
описания достаточно иметь частотные
характеристики в диапазоне частоты w
от
0 до
.
Чтобы выделить сигнал без искажения,
нужно, чтобы «боковые» спектры не
накладывались на основной спектр, для
этого необходимо, чтобы 0
2 нч.
Импульсная теорема сформулирована и доказана Котельниковым в 1933 году. В соответствии с этой теоремой, если сигнал не содержит частот выше, чем wнч, он полностью описывается своими значениями, измеренными в дискретные моменты времени с интервалом Т = / нч. Таким образом, период квантования должен быть:
Воспользуемся параметрами системы и выражением передаточной функции непрерывной части:
При помощи пакета Matlab определим нч:
Рис. 14. ЛАФЧХ непрерывной части
Получение передаточной функции сар в разомкнутом состоянии
Рассмотрим по структурной схеме получение передаточной функции разомкнутой импульсной САР.
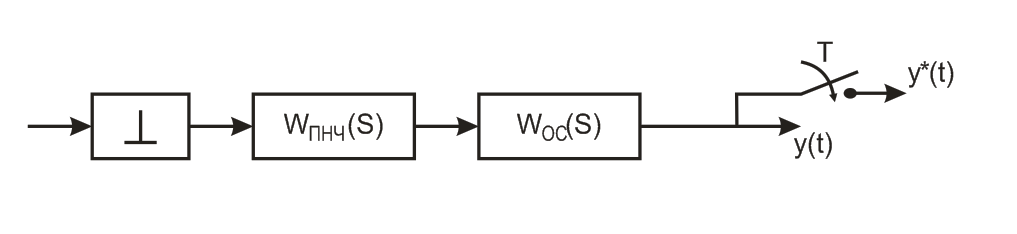
Рисунок 15. Структурная схема разомкнутой импульсной САР
=
При помощи пакет Matlab найдем
>> Wnch=tf([746.496 37.3248], [0.0504 12.604 1 0])
Transfer function:
746.5 s + 37.32
-------------------------
0.0504 s^3 + 12.6 s^2 + s – передаточная функция непрерывной части
>> Wos=tf([0.21], [0.014 1])
Transfer function:
0.21
-----------
0.014 s + 1 – передаточная функция обратной связи
>> W=Wnch*Wos
Transfer function:
156.8 s + 7.838
------------------------------------------
0.0007056 s^4 + 0.2269 s^3 + 12.62 s^2 + s – передаточная функция разомкнутой системы
>> Wrs=c2d(W,0.049)
Transfer function:
0.3928 z^3 - 0.1945 z^2 - 0.1963 z - 0.0005978
----------------------------------------------------
z^4 - 2.026 z^3 + 1.056 z^2 - 0.03009 z + 1.439e-007 - передаточная функция разомкнутой системы в дискретном виде
Получение передаточной функции сар в замкнутом состоянии
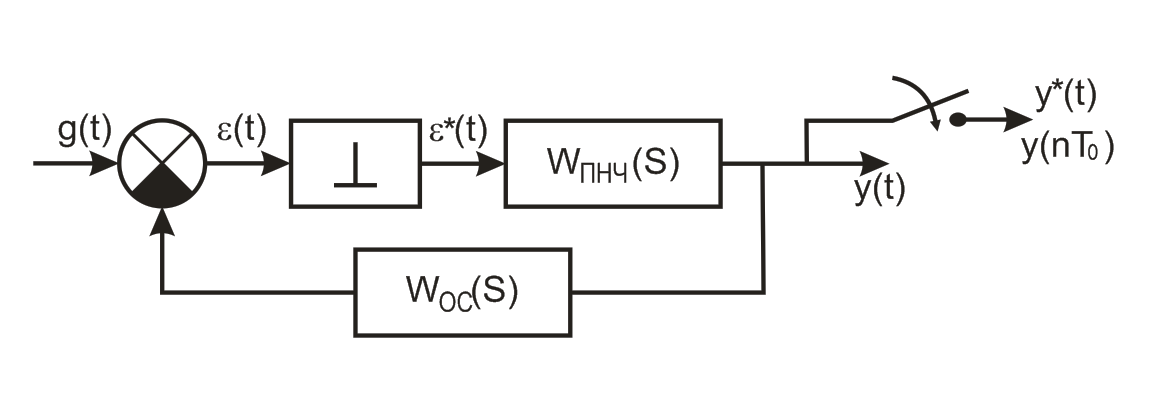
Рис. 16. Структурная схема замкнутой импульсной САР
=
При помощи пакет Matlab
найдем
>> Wnch=tf([746.496 37.3248], [0.0504 12.604 1 0])
Transfer function:
746.5 s + 37.32
-------------------------
0.0504 s^3 + 12.6 s^2 + s – передаточная функция непрерывной части
>> Wos=tf([0.21], [0.014 1])
Transfer function:
0.21
-----------
0.014 s + 1 – передаточная функция обратной связи
>> Wnchz=c2d(Wnch,0.049)
Transfer function:
2.664 z^2 - 2.421 z - 0.2361
---------------------------------------
z^3 - 1.996 z^2 + 0.9961 z - 4.767e-006 - передаточная функция непрерывной части в дискретном виде
>> Wosz=c2d(Wos,0.049)
Transfer function:
0.2037
----------
z - 0.0302 – передаточная функция обратной связи в дискретном виде
>> Wzs1=feedback(Wnchz,Wosz)
Transfer function:
2.664 z^3 - 2.502 z^2 - 0.163 z + 0.007129
------------------------------------------------
z^4 - 2.026 z^3 + 1.599 z^2 - 0.5232 z - 0.04808 – передаточная функция замкнутой системы в дискретном виде
>> Wzs=Wzs1*12
Transfer function:
31.97 z^3 - 30.02 z^2 - 1.956 z + 0.08555
------------------------------------------------
z^4 - 2.026 z^3 + 1.599 z^2 - 0.5232 z - 0.04808 – передаточная функция замкнутой системы в дискретном виде
Проверим САР на устойчивость при помощи корневого метода:
>> abs(pole(Wzs))
ans =
0.9976
0.8087
0.8087
0.0737
Чтобы замкнутая импульсная САУ была
устойчива, необходимо и достаточно,
чтобы корни характеристического
уравнения системы по модулю были меньше
единицы., то есть
,
если
- то система на границе устойчивости, а
если
- то система неустойчива [1].
Корни удовлетворяют условиям, следовательно, система устойчива.