21. Условия равновесия пар.

У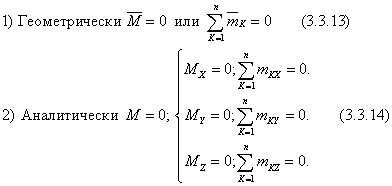 словия равновесия пространственной системы пар, запишутся:

Если в результате сложения пар , то действующие на тело пары образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением ,т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю. Значит, систему пар или одну пару можно уравновесить только парой.

22. Приведение силы к заданному центру.

Теорема о параллельном переносе силы: силу F, не изменяя ее действие на абсолютно твердое тело, можно переносить из данной точки (А) в любую другую точку (О) тела, прибавляя при этом пару с моментом (m), равным моменту переносимой силы относительно точки (О), куда сила переносится [m = m_o (F)]; F F, m.   Приведение системы сил F₁, F₂, ..., F_n к произвольном центру (точке) О, т. е. замене данной системы сил другой эквивалентной более простой, происходит с помощью Теоремы Пуансо: любая система сил F₁, F₂, ..., F_n действующих на абсолютно твердое тело, при приведении к произвольному центру О заменяется одной силой R, равной главному вектору системы сил, приложенной в центре О и парой сил с моментом M_o, равным главному моменту системы сил относительно центра (точки) О. Главный вектор:

R = F1 + F2 + ... + Fn  = ∑Fk, (k = 1, 2, ..., n)

а главный момент системы сил относительно центра (точки) О:

Mo = m1 + m2 + ... + mn = mo(F1) + mo(F2) + ... + mo(Fn) = mo(Fk).  (k = 1, 2, ..., n)

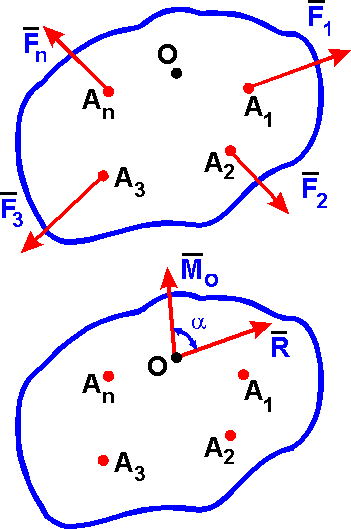     Величина главного вектора R не зависит от выбора центра О, а значение главного момента M_o при изменении положения центра О может в общем случае изменяться.   Для плоской системы сил F₁, F₂, ..., F_n главный вектор R лежит в плоскости действия сил, а главный момент  перпендикулярен этой плоскости ( = 90). Поэтому главный момент плоской системы сил относительно центра О определяется как сумма алгебраических моментов сил относительно точки (центра) О: M_o = m_o(F_k),     (k = 1, 2, ..., n) и изображается на плоскости дуговой стрелкой.

23. Приведение произвольной системы сил к силе и паре сил ( основная теорема статики). Теорема Пуансо.

Пусть дана произвольная система сил (F₁, F₂,..., F_n). Сумма этих сил F=åF_{k -} главный вектор системы сил. Сумма моментов сил относительно какого-либо полюса - главный момент рассматриваемой системы сил относительно этого полюса. Осн теор статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, прило­женной в какой-либо точке тела (центре приведения) и равной глав­ному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.

Пусть О — центр приведения, принимаемый за начало коорди­нат, r₁,r₂, r₃,…, r_n–соответствующие радиусы-векторы точек приложения сил F₁, F₂, F₃, ...,F_n, составляющих данную систему сил (рис. 4.2, а). Перенесем силы F₁, F_a, F₃, ..., F_n в точку О. Сложим эти силы как сходящиеся; получим одну силу: F_о=F₁+F₂+…+F_n=åF_k, которая равна главному вектору (рис. 4.2, б). При последователь­ном переносе сил F₁, F₂,..., F_n в точку О получаем каждый раз соответствующую пару сил (F₁, F”₁), (F₂,F”₂),...,(F_n, F"_n).Моменты этих пар соответственно равны моментам данных сил относительно точки О: М₁=М(F₁,F”₁)=r₁ x F₁=М_о(F₁), М₂=М(F₂, F”₂)=r₂ x F₂=М_о(F₂), …, М_п=М(F_n, F"_n)=r_n x F_n=М_о(F_n). На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т. е. равен главному моменту, М₀=М₁+М₂+...+М_n=М_о(F₁)+М_о(F₂)+…+ М_о(F_n)==åМ_о(F_k)=år_k x F_k. Систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой F_o=åF_k и парой сил с моментом M₀=åM₀(F_k)=år_k x F_k.

24. Формулы для определения главного вектора и главного момента в декартовой системе координат.

Выбираем систему координатных осей Oxyz и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:

П о найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R . Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами: Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента:

Главный момент, по определению, есть векторная сумма моментов всех сил центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:

Косинус угла между главным вектором и главным моментом определяется так: Отсюда:

25. Зависимость главного момента от выбора центра приведения.При переходе от одного центра приведения к другому изменяется момент произвольной силы F_{i ,} выражения для моментов силы относительно каждого из центров:

1. Между собой точки приведения A и B связаны радиус-вектором d:

2. Радиус-вектор r_Bi в выражение для момента силы M_B(F_i):

3. Просуммируем моменты всех сил M_B(F_i):

4. Получили зависимость главного момента сил от выбора центра приведения:

главный минимальный момент выражается через скалярное произведение:

Главный минимальный момент может быть вычислен как проекция главного момента в любой точке приведения на центральную ось: