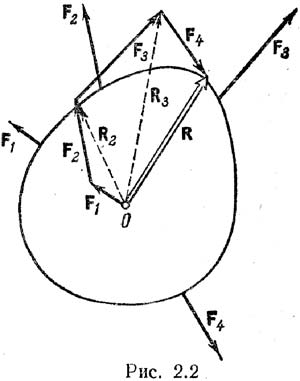
7.Приведение системы сходящихся сил к равнодействующей.

С истема сходящихся сил эквивалентна одной силе (равнодейству­ющей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия. Пусть задана система сходящихся сил F₁, F₂, F₃, ..., F_n, при­ложенных к абсолютно твердому телу . Перенесем точки приложения сил по линиям их действия в точку пересечения этих линий . Получили систему сил, приложенной к одной точке. Она эквивалентна заданной. Сложим F₁ и F₂, получим их равнодействующую: R₂=F₁+F₂. Сложим R₂ с F₃: R₃=R₂+F₃=F₁+F₂+F₃. Сложим F₁+F₂+F₃+…+F_n=R_n=R=åF_i. Вместо параллелограммов можно построить силовой многоугольник. Пусть система состоит из 4 сил . От конца вектора F₁ отложим вектор F₂. Вектор, соединяющий начало О и конец вектора F₂, будет вектором R₂. Далее отложим вектор F_3, помещая его начало в конце вектора F₂. Тогда мы получим вектор R₈, идущий от точки О к концу вектора F₃. Точно так же добавим вектор F₄; при этом получим, что вектор, идущий от начала первого вектора F₁ к концу вектора F₄, является равнодействующей R. Такой пространственный многоугольник называется силовым. Если конец последней силы не совпадает с началом  первой силы, то силовой многоугольник - разомкнутый.

Графический и аналитический способы нахождения равнодействующей.

При графическом способе определения равнодействующей век­торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

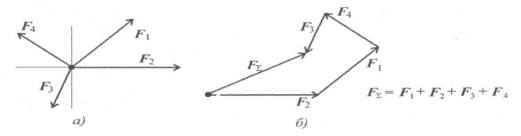
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим. При вычерчивании многоугольника необходимо обращать внимание на параллельность сторон многоугольника соответствую­щим векторам сил.

А налитическое определение равнодействующей – каждая из сил, геометрическая сумма которых дает равнодействующую, может быть представлена через ее проекции на координатные оси и единичные векторы (орты): Тогда равнодействующая выражается через проекции сил в виде: Группировка по ортам дает выражения для проекций равнодействующей: Отсюда проекции равнодействующей:

Направляющие косинусы равнодействующей :

Модуль равнодействующей:

8. 9.Алгебраический способ нахождения равнодействующей.

Аналитическое определение равнодействующей – каждая из сил, геометрическая сумма которых дает равнодействующую, может быть представлена через ее проекции на координатные оси и единичные векторы (орты):

Тогда равнодействующая выражается через проекции сил в виде: Группировка по ортам дает выражения для проекций равнодействующей: Отсюда проекции равнодействующей:

Направляющие косинусы равнодействующей :

М одуль равнодействующей:

10.Геометрическое и аналитическое условие равновесия системы сходящихся сил.

Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.

1.Геометрическое условие равновесия. Для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут. Условия равновесия плоской системы сходящихся сил в аналитической форме: Исходя из того, что равнодействующая равна нулю, получим:

F _Σ = 0. Условия равновесия в аналитической форме : плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю. Система уравнений равновесия плоской сходящейся системы сил: