5.2. Статистическое распределение выборки

Пусть требуется изучить совокупность однородных объектов (генеральную совокупность) относительно некоторого признака .

Извлечем из генеральной совокупности выборку.

При этом оказалось, что значение случайной величины , равное , наблюдалось раз, значение – раз, …, – раз. Объем выборки .

Наблюдаемые значения есть варианты, а последовательность вариант, записанных в возрастающем порядке, есть вариационный ряд. Числа наблюдений , есть частоты, а их отношение к объему выборки – относительные частоты.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот (или относительных частот).

Статистическое распределение выборки можно задать в виде таблицы, в первой графе которой располагаются варианты , а во второй – соответствующие этим вариантам частоты или относительные частоты .

Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот. При этом в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал.

Для графического изображения статистического распределения выборки в случае дискретного распределения признака строят полигон частот, а в случае интервального распределения признака строят гистограмму.

5.3. Показатели вариации признака

Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.

Вариационные ряды характеризуются различными показателями.

Важной характеристикой вариационного ряда (выборки) является среднее арифметическое наблюдаемых значений признака, то есть выборочная средняя :

.

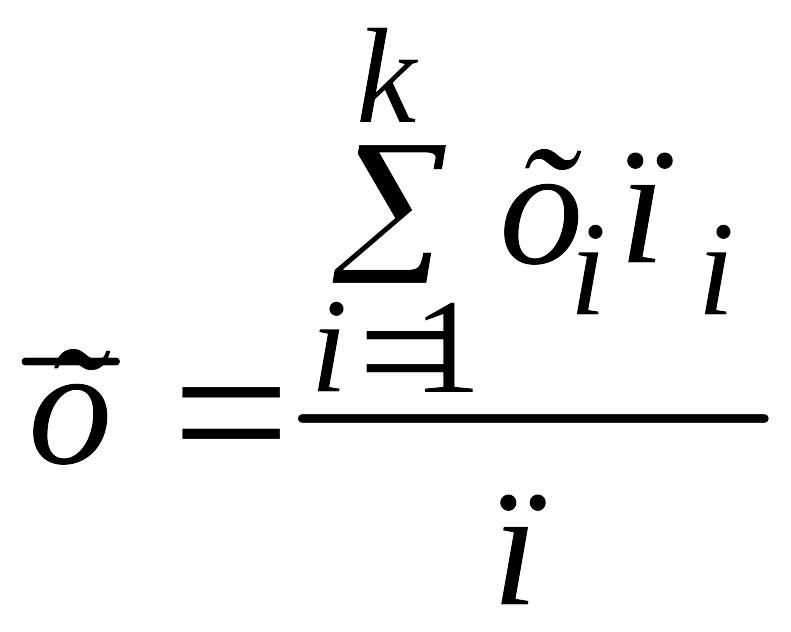При оценке результатов статистического наблюдения всегда применяют выборочное среднее, которое в случае, когда наблюдений достаточно много, представляет собой хорошее приближение для генеральной средней (средней арифметической генеральной совокупности).

Однако выборочное среднее может раскрыть лишь общую тенденцию изучаемого явления и только тогда, когда она выведена из большого числа наблюдений и при наличии однородной совокупности.

Средняя величина не показывает строения совокупности, которое весьма существенно для ее познания. Она не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Одинаковые средние могут иметь совершенно разнородные совокупности.

Колеблемость отдельных наблюдаемых значений изучаемого признака характеризуют показатели вариации.

Наиболее простой параметр изменения разброса значений варьирующего признака – размах вариации (размах колебаний).

Размах вариации – это разность между наибольшим и наименьшим значениями вариант:

.

Размах вариации улавливает только крайние отклонения, но не отражает отклонений от средней всех значений признака в вариационном ряду.

Чтобы дать обобщающую характеристику распределению отклонений, вычисляют среднее линейное отклонение, которое учитывает различия всех единиц изучаемой совокупности.

Среднее линейное отклонение определяется как средняя арифметическая отклонений индивидуальных значений вариант от средней, без учета знака этих отклонений:

.

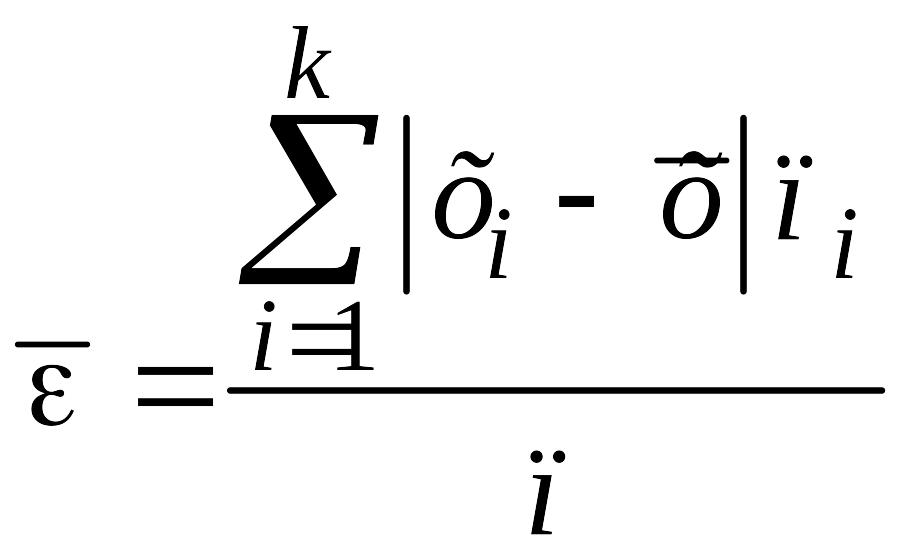Среднее линейное отклонение как меру вариации признака применяют в статистическом анализе редко.

Более объективно отражает меру вариации показатель вариации, называемый дисперсией.

Дисперсия представляет собой среднее арифметическое отклонений индивидуальных значений вариант от средней, возведенных в квадрат:

.

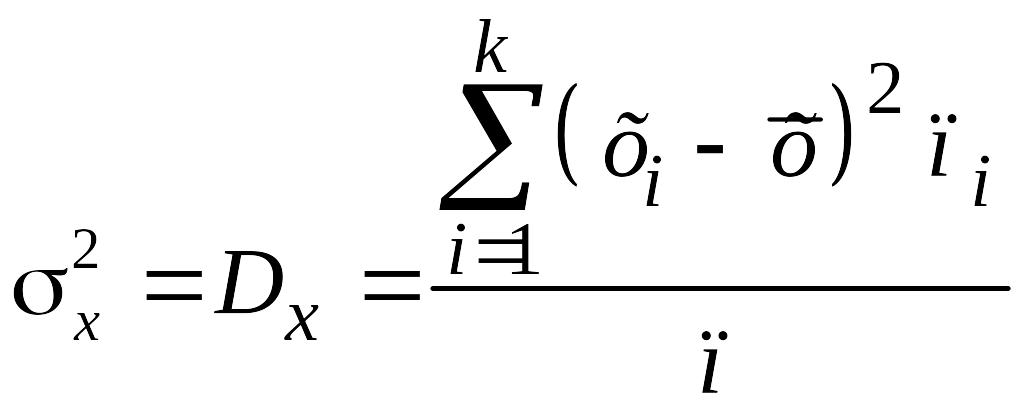Чем больше дисперсия, тем больше разброс вариант относительно средней.

Средним квадратическим отклонением называют корень квадратный из дисперсии.

.

Среднее квадратическое отклонение всегда имеет ту же размерность, что и случайная величина (изучаемый признак).

Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю изучаемую совокупность (выборку).

Для характеристики меры вариации изучаемого признака в относительных величинах вычисляют относительные показатели вариации. Они позволяют сравнивать характер рассеивания в вариационных рядах различной размерности с разными уровнями.

Коэффициент осцилляции определяется по формуле

.

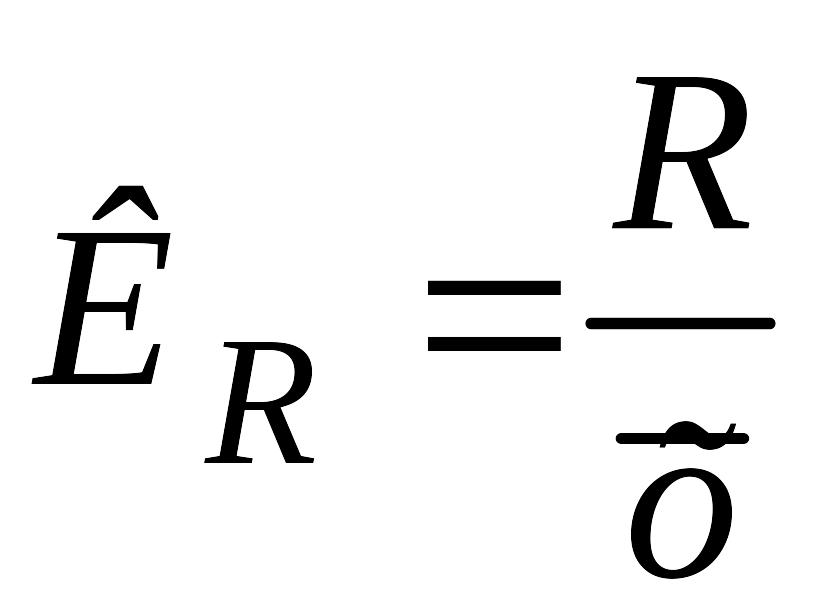Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

Относительное линейное отклонение вычисляется по формуле

.

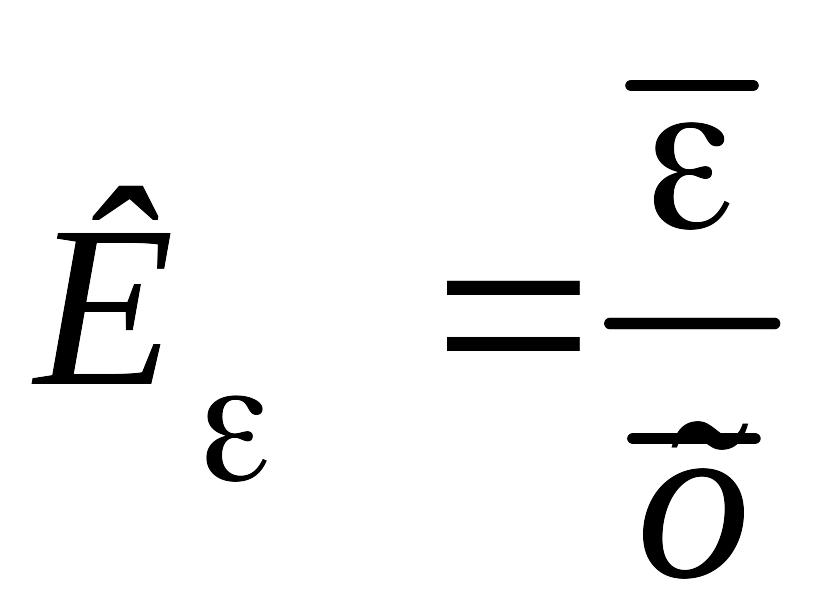Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.

Коэффициент вариации определяется по формуле

.

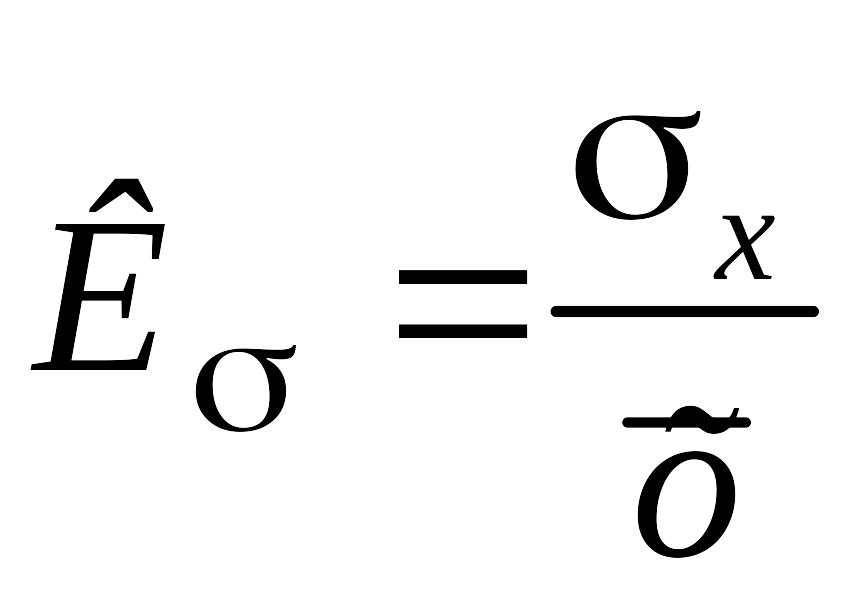Учитывая, что среднее квадратическое отклонение дает обобщающую характеристику колеблемости всех вариант вариационного ряда, коэффициент вариации является наиболее распространенным показателем вариации, используемым для оценки типичности средних величин. При этом исходят из того, что если , то это говорит о большой колеблемости значений признака в изучаемой совокупности.

Относительные показатели вариации часто измеряются в процентах.