Определение масштаба карты, главного, частного масштаба. Виды масштабов.
Масштаб можно записать в виде дробного числа, например — 1:10 000.
Масштаб, выраженный дробью, называется численным.
Число 1 (числитель дроби) — это расстояние на плане, которое соответствует 10 000 (знаменатель) таких расстояний на местности (т. е. 1 см на плане равен 10 000 см на местности).
В численном масштабе числитель всегда равней единице, а знаменатель — числу, которое показывает, во сколько раз расстояние на плане меньше, чем на местности.
Важно помнить, что в численном масштабе оба числа всегда даны в сантиметрах.
Пользуясь численным масштабом удобно определять, во сколько раз уменьшено расстояние на плане.
Часто рядом с численным масштабом приводят его пояснение.
Например, в 1 см - 100 м (т. е. 10 000 см для удобства преобразовано в метры).
Это означает, что 1 см на плане соответсвует 100 м на местности.
Масштаб, записанный словами, называется именованным (или словесным).
Расстояние на местности, которое соответствует 1 см на плане, называют величиной масштаба.
С помощью величины масштаба удобно определять расстояния.
Например, какова длина школьного стадиона, если его длина на плане — 5 см, а величина масштаба — 100 м?
Легко вычислить, что длина стадиона составляет 500 м
(5 см х 100м = 500 м).
Как преобразовать численный масштаб в именованный?
Например, численный масштаб 1: 25 000.
Преобразуем 25 000 см в метры (25 000 см : 100 000 = 0,25 км = 250 м).
Следовательно, именованный масштаб такой: в 1 см - 250 м.
На планах размещают также и линейный масштаб.
Его изображают в виде прямой линии, разделённой на равные части (обычно на сантиметры).
Около каждого деления-линии подписывают соответствующее масштабу расстояние на местности (например: 100,200,300м,...).
При этом ноль ставят, отступив на 1 см от левого края отрезка. А первый сантиметр делят на миллиметры (которые соответственно обозначают 10, 20, 30 м, ... на местности).
С помощью линейного масштаба можно быстро и легко измерить расстояние и, пользуясь циркулем-измерителем, определить размеры объектов на плане.
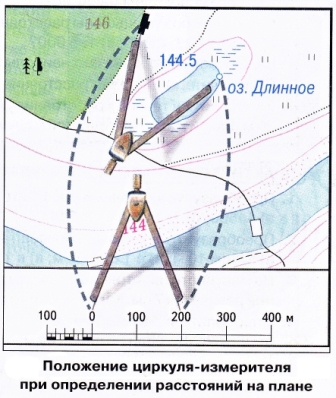
МАСШТАБотношение длины данной линии на чертеже, плане или карте к ее длине на местности. Различают главные и частные масштабы. ГЛАВНЫЙ МАСШТАБ указывается (подписывается) на карте; он представляет собой степень уменьшения земного шара до размеров глобуса, поверхность которого переносится на карту. Главный масштаб остается неизменным вдоль одной или нескольких линий (меридианов или параллелей) . Частный масштаб (в данной точке) - это отношение длины бесконечно малого отрезка на карте к соответствующей длине бесконечно малого отрезка на местности. На планах, охватывающих малую часть земной поверхности, масштаб практически повсюду постоянен.
Классификация проекций по характеру искажений. Их краткая характеристика.
а) равноугольные, или конформные оставляют без искажений углы и форму контуров, но имеют значительные искажения площадей. Элементарная окружность в таких проекциях всегда остается окружностью, но размеры ее сильно меняются. Такие проекции особенно удобны для определения направлений и прокладки маршрутов по заданному азимуту, поэтомy их всегда используют на навигационных картах.,
Эти проекции могут быть описаны уравнениями в характеристиках вида:
m=n=a=b=m
q=900 w=0 m=n
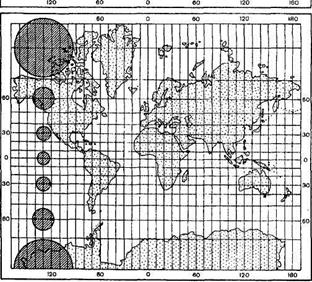
Рис. Искажения в равноугольной проекции. Карта мира в проекции Меркатора
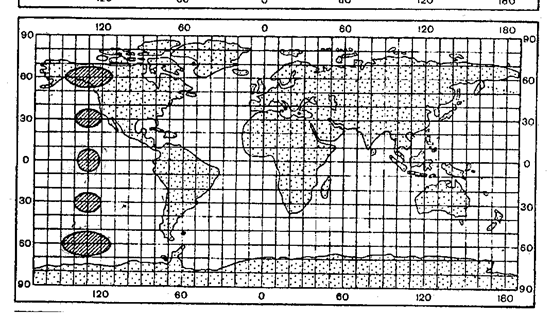
б) равновеликие, или эквивалентные - сохраняют площади без искажений, однако на них значительно нарушены углы и формы, что особенно заметно на больших территориях. Например, на карте мира приполярные области выглядят сильно сплющенными. Эти проекции могут быть описаны уравнениями в характеристиках вида..
Они описываются характеристическими уравнениями вида Р = 1,
Рис. Искажения в равновеликой проекции. Карта мира в проекции Меркатора
в) равнопромежуточные(эквидистантные).
В этих проекциях линейный масштаб по одному из главных направлений постоянен и обычно равен гл. м. карты, т. е. имеет место
либо а = 1, либо b = 1;
г) произвольные.
Не сохраняют ни углов, ни площадей.