Государственно-образовательное учреждение высшего профессионального образования Московской области

Международный университет Природы, Общества и Человека «Дубна»

Кафедра Персональной Электроники

Курсовая работа

по дисциплине

“Математические методы в электронике”

Тема: «Моделирование процессов в электрических цепях на основе дифференциальных уравнений»

Выполнил:

студент 2 курса группы № 2142

Донгузов Илья Игоревич

Руководитель: проф. Трофимов А. Т.

Дубна, 2014

Оглавление

Вывод дифференциального уравнения 4

Моделирование процессов, происходящих в цепи, в системе математического моделированя MathCAD 6

Решение неоднородного дифференциального уравнения, описывающего завсимость выходного сигнала от входного, при подаче на вход цепи сигнала, имеющего вид единичного скачка напряжения. Выходное напряжение цепи в момент времени t = 0 равно (Y(t)=0). 6

Решение однородного дифференциального уравнения, описывающего завсимость выходного сигнала от времени, при условии, что выходное напряжене цепи в момент времени t=0 равно (Y(t)=1). 8

Наити решение неоднородного дифференциального уравнения описывающего завсимость выходного сигнала от входного, при подаче на вход цепи сигнала, имеющего вид продифференцированного гауссовского импульса. Напряжение цепи в момент времени t=0 равно (Y(t)=0). 9

Основные выводы 12

Государственное бюджетное образовательное учреждение

высшего профессионального образования Московской области

Международный университет Природы, Общества и Человека «Дубна»

Кафедра Персональной Электроники

ЗАДАНИЕ

на курсовую работу по дисцеплине «Математические методы в электронике»

Тема курсовой работы:

Моделирование процессов в электрических цепях на основе дифференциальных уравнений.

Задачи, решаемые в работе:

1. Составить дифференциальное уравнение, описывающие зависимость выходного сигнала от входного сигнала в заданной электрической цепи.

2. Наити решение неоднородного дифференциального уравнения, описывающего зависимость выходного сигнала от входного, при подаче на вход цепи сигнала, имеющего вид единичного скачка напряжения. Выходное напряжение цепи в момент времени t = 0 равно (Y(t)=0).

3. Наити решение однородного дифференциального уравнения, описывающего зависимость выходного сигнала от времени, при условии, что выходное напряжение цепи в момент времени t=0 равно (Y(t)=1).

4. Наити решение неоднородного дифференциального уравнения, описывающего зависимость выходного сигнала от входного, при подаче на вход цепи сигнала, имеющего вид производной от функции Гаусса.

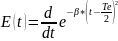
Напряжение на цепи в момент времени t=0 равно (Y(t)=0).

5. Привести графики выходных сигналов и сделать вывод о прохождении сигнала через соответствующую цепь.

Исходные данные:

1. Входной сигнал имеет форму:

1.1. Функция Хевисайда ( Единичного скачка).

1.2. Продифференцированного гаусовского сигнала c параметрами: длительность (Te) = 2 секунды, отношение сопротивление/индуктивность

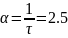
2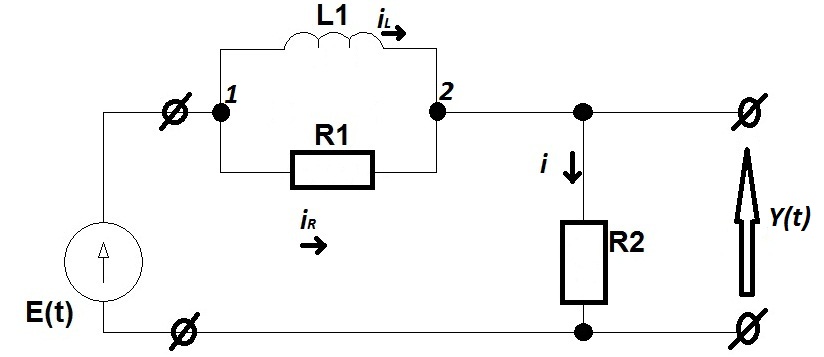 . Вид цепи:

Дата выдачи задания 25.04.2014

Дата защиты____________

Студент гр. 2142 Донгузов И.И.___

Преподаватель: проф. Трофимов А.Т.___

Вывод дифференциального уравнения

Обозначим ток, текущий через катушку 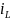, ток через резистор R1 обозначим как 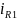, ток, протекающий через резистор R2, обозначим i.

Напряжение на концах катушки (и резистора R1) обозначим U. Искомое напряжение на концах резистора R2 обозначим как Y.

(Рисунок №1) Исследуемая цепь

Процессы, происходящие в цепи, описываются дифференциальным уравнением первого порядка, составленным с помощью первого и второго закона Кирхгофа.

1. Первое правило Кирхгофа гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю.

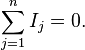
При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным. Иными словами, сумма втекающих токов равна сумме вытекающих токов. Это правило следует из фундаментального закона сохранения заряда.

2. Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю.

 

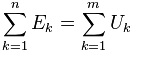
Для нашей схемы законы Кирхгофа записываются следующим образом:

Первый закон Кирхгофа:

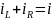……………………………………………(1)

Второй закон Кирхгофа:

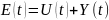…………………………………(2)

На основе второго закона Кирхгофа (2) получим:

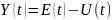....................................................(3)

Ток, протекающий через катушку:

……………..………………..….…..(4)

Подставим ток, выраженный через напряжение в уравнение (1), полученное по первому закону Кирхгофа.

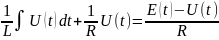………………………..…….(5)

Перенесём из правой части в левую и разделим обе части уравнения на . Получим:

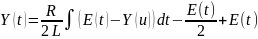……..........….(6)

Выполним дифференцирование и сделаем замену

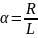
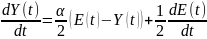………………..…………(7)

Полученное уравнение (7) является неоднородным дифференциальным уравнением первого порядка, описывающим зависимость выходного напряжения от входного для заданной цепи.

Моделирование процессов, происходящих в цепи, в системе математического моделированя MathCad

Решение неоднородного дифференциального уравнения, описывающего завсимость выходного сигнала от входного, при подаче на вход цепи сигнала, имеющего вид единичного скачка напряжения. Выходное напряжение цепи в момент времени t = 0 равно (Y(t)=0).

- Аналитическая форма сигнала

(Рисунок №2) График входного сигнала (единичный скачек напряжения).

Решение неоднородного дифференциального уравнения в системе математического моделрования MathCad (переходный процесс)

При моделировании данного процесса, необходимо учесть то, что выходное напряжение в момент времени t=0 равно Y(0) = 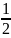. Это есть следствие того, что в начальный момент времени ток через катушку не протекает, так как ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию. Таким образом, ток протекает через два одинаковых по величине сопротивления, включённых последовательно. Тогда, данное включение сопротивлений работает как делитель напряжения, и выходное напряжение будет равно половине от входного.

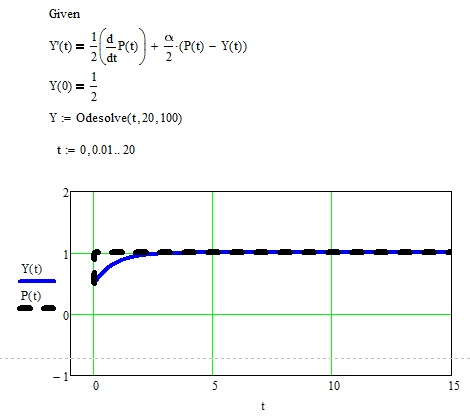
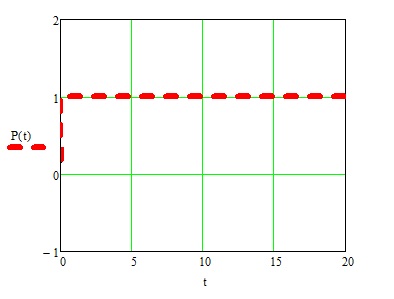
(Рисунок №3) График выходного сигнала (единичный скачек напряжения).

Вывод: на графике можно заметить, как после подачи единичного скачка напряжения на цепь происходит мгновенное увеличение выходного напряжения до , по причине того, что в начальный момент времени ток через катушку не протекает, и два одинаковых по величине сопротивления, соединённые последовательно, делят входное напряжение пополам. Далее, мы наблюдаем постепенное увеличения выходного напряжения и установление его стабильного состояния. Такой эффект мы наблюдаем так как скорость изменения тока через катушку ограничена и определяется индуктивностью катушки. При подключении источника питания, ток через индуктивность возрастает постепенно, и скорость изменения тока зависит от величины индуктивности.

Решение однородного дифференциального уравнения, описывающего завсимость выходного сигнала от времени, при условии, что выходное напряжене цепи в момент времени t=0 равно (Y(t)=1).