2. Числовые ряды.

ОПР: Числ ряд – это сумма членов числпоследовательности вида: (1)

ОПР: Сумма n первых членов ряда называется n-ой частичной суммой и обозначается символом Sn:Sn = u1 + u2 + … + un.

ОПР: Если для последовательности Sn частичных сумм существует конечный предел S, то ряд (1) наз сход-ся, а число S — суммой данного ряда. В этом сл пишут: ; .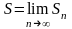

ОПР: 4 Ряд (1) называется расходящимся, если 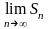не существует или бесконечен.

Т: Если ряд (1) сходится, то его общий член стремится к нулю: .

СЛ: Если то ряд расходится.

Приз сход числ рядов. Критерий Коши: для того, чтоб ряд(1) сход , необ и достат, чтоб при такой номер N=N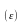 , что при 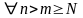вып При m+1=n полу приз сход (1): неох усл: если ряд(1) сход, то 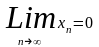(обрат утвержд не верно).

Достат усл: Из при n>m след, что из сход-ти 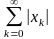(2)вытек сход ряда . Если ряд (2) сход, то ряд(1) сход абсолют. Если ряд (1) сход, а (2) расход, то ряд (1) наз условно сход.

Теорема. Имеют место след приз сход и расх (1):

1. Пусть , гдеС=const, тогда (1) сход абс Док-во: пусть образ неубыв послед, огран-ю свер, поэт послед

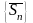
сход, т.е. ряд (1) сход.

2. (признак Коши). Пусть , тогда ряд (1) сход абс при и расход при .

3. (приз Даламбера). Пусть , тогда ряд(*) сход абс при , если же при имеет место 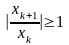, то ряд (1) расход.

Признак Лейбница. - ряд со знакочеред-ся числ, т.е. , тогда если при -монотон невозр и 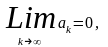, то ряд (1) сход.

2. Функциональные последовательности.

Пусть {fn(x)} — последовательность функций, каждая из которых определена на некотором подмножестве X ⊂ R. В этом случае говорят, что на множестве X задана функциональная последовательность {fn(x)}. (n пишется как индекс при f).

ОПР: Функциональная последовательность {fn(x)} называется сходящейся на множестве X к функции f(x), если в каждой точке x ∈ X числовая последовательность {fn(x)} сходится к f(x).

ОПР: Говорят, что посл-сть {fn(x)} равномерно сходится на мн-ве X к ф-ии f(x), если для любого ε > 0 найдется такой номер nε, что для всех n > nε и при любом x ∈ X выполняется

неравентсво|fn(x) − f(x)| < ε. В этом случае пишут fn(x) ⇒ f(x) на X. (nε—эпселент пишите кА книжний индекс при n).

Т 1. (крит Коши равномерной сходимости):Для того, чтобы посл-сть {fn(x)} равномерно сходилась на мн-ве X, необхо и достат, чтобы для любого ε > 0 существовал такой номер N = N(ε), что при всех n, m > N(ε) и любом x ∈ X выполнялось неравенство|fn(x) − fm(x)| < ε. (1)

Пусть дана некот функц посл {fn(x)} сходящаяся на данном множестве Д к ф-ции f(x). Будем считат, что все функции fn(x), n=1,2,3 .. непрер на множ Д:

Т (о непрерывности предельной функции): Если посл-ть {fn(x)} непрерывных на мн-ве Д функций сход-ся на этом множестве к некот ф-ции f(x) равномерно, то и предельная ф-ция f(x) непрерывна в области Д.

Пусть на [a,b] определена сходящаяся посл-ть ф-ций f₁(x), f₂(x),…(4) и пусть f(x) явл предельной функцией этой посл-ти:

Т(о переходе к пределу по знаком интеграла): Если посл-ть (4) состоящая из непрер на [a,b] функций равномерно сх-ся на [a,b] к некот ф-ции f(x), то имеет место равенство: .

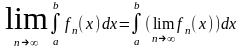Пусть сходящаяся в обл Д к некот функции f(x) посл-ть {fn(x)} состоит из дифф-мых в этой области функций. Можно рассмотреть посл-ть {fn'(x)}:

Т(о переходе к пределу под знаком производной): Если функц посл-ть {fn(x)} удовл след условиям: 1) она сходится на данном отрезке [a,b] к функции f(x). 2) члены этой посл-ти имеют на указанном отрезке непрер производные. 3) послед-ть {fn’(x)}этих производных сх-ся на [a,b] равномерно к некот ф-ции f(x), то имеет место соотношение: F(x)=f ‘ (x), т.е.