2. Дифференцирование функций многих переменных.

Функцией многих перем наз отображение f: X→Rⁿ , n – координат, для ф-ции y=f(x), где х=(x1,x2,…,xn). Ф-ция двух перем имеет вид z=f(x,y) для R².

Предпол, что переменная х1, а остальные фиксированные.

1.х1, x0 тогда ф-я получ частное приращение.

2.f=f(х1+х1, х2,…,хn)-f(x1,x2,…xn) – полное приращение.

Опр. Если сущ предел отношения частного приращения ф-и к вызванному приращению аргумента, то этот предел наз. частной производной от ф-и f по перем х1.

Пример. z=5x²y-x³

Опр. ф-я у=f(x1 x2 ….xn) наз. диффер.в т. х=(х1…хn) если ее полное приращение ф-ции у=f(х1+х1, х2+х2,…,хn+хn)-f(x1,x2,…xn) представимо в виде

А₁х₁+..+A_nx_n+₁(x) x₁+…+_n(x) x_n.где _i-б/м.

Теор.(необх.усл.)

Если ф-ция y=f(x1...xn) дифферен. В некоторой т х0=(х1^0,...xn^0) то сущ. В этой точке все частные производ. И соотв. Равны постоян. Аi т.е.df/dx1(x0)=A1,...df/dxn(x0)=An.

Док-во:

Т.к. f диф. в т х0 по опред.

f = А1 f = А1х1+..+х1+..+Anxn+1(x) x1+

+…+n(x) xn.где i-б/мх1-перемен.

х2... хn=0(положим).

f=A1 x1+1x1, f/x1=A1x1/x1+1x1/x1=A1+1

т.к. предел правой части сущ. U=A1 то левой

части сущ. U=A1 а по опр.

lim f/x=df/dx1(x0)=A1 ч.т.д.

Теор.(достат.усл.)

Если y=f(x1...xn) имеет частные произ. В некот. Окрестности т. Х₀ , а в самой точке эти производ. Непрерыв. То ф-ция f(x) диференц.в т. Х₀.

Теор. Если ф-ция F(x,y)

А)им непрер част произв F_x^’(x,y),F_y^’(x,y) в нек-й U(x0,y0)

Б)F(x0,y0)=0

В) F_y^’(x0,y0)0

То сущ прямоуг область П{(x,y)/x-x0a, y-y0b}такой что ур-ние F(x,y)=0 опред. В нем у как неявную ф-цию от х и ф-ция непрер. на [х0-a,х0+а] и диффер. на (х0-a,х0+а) т.е. f^’(x)=-( F_x^’(x,f(x))/ F_y^’(x,f(x)))

Т. о неявной функции.

F(x)=y,Y’(x)=limy/x x0 y=f(x1,x2,…,xn) f:Rⁿ R

2. Основные теоремы о дифференцировании функций многих переменных.

ОПР: Пусть ф-ция F(x,y) определена на некот мн-ве Д изменения переменных х и у, и пусть на каком-либо мн-ве Е знаечний х, таких что х,у принадл , а х принимает какое-то значение из Д, сущ такая функция у=f(x), которая будучи подставленной в уравнение F(x,y)=0 вместо у обращает это уравнение на мн-ве Е в тождество относительно х, т.е. F(x,f(x))≡0. Тогда говорят, что на данном мн-ве Е ф-ция у=f(x) задана неявно.

Т1:(о непр-сти дифф функции):Всякая дифференцируемая функция непрерывна.

Т2(необх усл дифф-сти):Если функция z=f(x,y) дифференцируема в точке   (x0,y0), то в этой точке сущ частные произв по всем переменным и они равны: ;

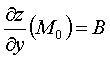
Т3 (достатусловие дифференцируемости):Пусть в области D функция z=f(x,y) имеет непрерывные частные производные, тогда функция дифференцируема.

Теорема 1 (Формула Тейлора для функций многих переменных).  Пусть        m+1  раз  дифференцируемая  функция в области D, точки х,х0 принадл Д, причем  отрезок прямой     соединяющий точки   целиком лежит в  D. Тогда справедлива  формула где        некоторое число.  Поскольку под знаком  суммы   , то  имеем

ОПР: Пусть дана ф-ция z=f(x,y) в окр обл Д. Будем гов, что ф-ция z=f(x,y) имеет max в m(x0, y0), если знач ф-ции в некот окр данной точки не превышают значения функции в самой этой точке, т.е. выполн нер-во: f(x,y)≤f(x0,y0) для любой точки принадл окрестности т (х0,у0).

ОПР: Пусть дана ф-ция z=f(x,y) в окр обл Д. Будем говорить, что ф-ция z=f(x,y) имеет min в m(x0, y0), если знач ф-ции в некот окр данной точки меньше значения функции в самой этой точке, т.е. выполн нер-во: f(x,y)≥f(x0,y0) для любой точки принадл окрестности т (х0,у0).

Т (необх усл сущ-ния экстр): Если ф-ция z=f(x,y) опред в некот обл Д, имеет экстремум в т (х0, у0), то 1-ые частные произв данной ф-ции в этой точке образуются в нуль (если они сущ).

Достаточные условия сущ-ния экстремума: Пусть функция y = f(x) непр на всем инт (a, b), дифф-ма на (a, b), кроме, быть может, числа x0 (a,b), причем точка (x0, f(x0)) является критической точкой графика функции f. Тогда, если при переходе через x0 произв меняет знак с плюса на минус (с минуса на плюс), то f'(x0) – максимум (минимум) функции f.

ОПР: Условным экстр ф-ции   в т   наз экстр этой ф-ции, достигнутый при условии, что перем x и у в окр данной точки удовлетворяют уравнению связи  .

Метод множ Лагранжа Для отыскания условного экстр составляют ф-цию Лагр: .Необхусл экстр задаются систуравн, из кот опред стационарные точки:

       Достаточным условием, из которого можно выяснить характер экстремума, служит знак  . Если в стационарной точке  , то функция   имеет в данной точке условный минимум, если же  , то условный максимум.