2. Методика изучения многогранников и их свойств.

Рассмотрение многогр-ов в начале курса имеет ряд преимуществ методического хар-ра: 1)позволяет осознанно изучать акс. и их сл-ия; 2)пробуждает интерес к изучению предмета; 3)способствует лучшему усвоению теорет. и практич. материала; 4)позволяет перейти к графическому моделированию необх. в любой обл-ти интеллект-ой дея-ти; 5)позволяет преодолеть формализм в обучении. Особенности изучения призмы: А.В.Погорелов: Призма – это мн-ник, состоящий из 2 многоуг-ов, лежащих в разных пл-тях и совмещаемых параллельным переносом, и всех отрезков соединяющих соотв-ие т-ки этих многоуг-ов. В.В.Шлыков: Призма – это многоуг-ик, у кот. 2 грани равные n-угольники (назыв. основан.) с соотв-но параллельными сторонами( параллельно 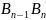) , а остальные n-граней – параллелограммы, у каждого из которых 2 стороны являются соотв-ми сторонами оснований. Для запоминания полезно выделить составные элем-ты опр-ия. Для слабых учащ-ся достаточно сформулировать опр-ие призмы данное в 10 кл.: призма – это мн-к, у кот. 2 грани равные n-угольн., а остальные грани – параллелограммы. Затем вводится понятие прямой и наклонной призмы. Поск.наглядное представление о пирамиде у учащ-ся есть, в 10 кл. давалось опр., то учителю остаётся актуализировать знания. Пирамида – мн-к, у кот., одна грань некоторый n-угольник а остальные грани – треугольники с общей вершиной O. В 10 кл. это же опр. даётся без обозначения, для лучшего запоминания можно не требовать предшествующей формулировки. В уч.Шл. это заполненная фигура, у большинства авторов шк.учебн. это полная фиг. или пов-ть. Погорелов: Пирамида – это мн-к, который состоит из плоского многоуг-ка, т-ки лежащей вне пл-ти и всех отрезков, соединяющих данную т-ку с т-ми основания. Элем-ми пирамиды явл-ся: основание, боковое ребро, вершина, высота, полная пов-ть, боковая пов-ть и их площади, диагональное сечение. Наиболее сложными среди них явлся понятие вершины, она одна и наз-ся и записывается первой в обозначении пирамиды; высота пирамиды – опр-ие основания высоты в различного вида пирамидах. Для характерных случаев расположения высоты пирамиды полезно одновременно рассм-ть 3 задачи: боковые рёбра равны, двугранные углы при рёбрах основания равны, боковые рёбра одинаково наклонены к пл-ти основания. Полезно рассмотреть частные случаи, когда в основании лежат прямоуг., равнобедр. и равностор. треугольники.

2. Методика изучения тел вращения, их св-в.

Тема изучается в 11 кл (16ч) после темы "многогранники". По логике изучения многогр. (призма - пирамида - прав многогранники - фигуры вращения) должны изучаться в след порядке: цилиндр - конус - сфера - шар. Авторы учебников, в кот принят такой порядок, мотивируют это доступностью для уч-ся, т.к. соответствующие фигуры имеют много общих св-в.

В уч. пособ. Шл. принят след порядок изучения: сфера - шар - цилиндр - конус - усеч конус. Мотивация: 1) можно ввести используя аналогию с понятиями окр. и круг. 2) большой временной промежуток для их изучения. 3) изучение вопросов, связанных с впис. и опис. многогр. 4) отработка навыков нахождения центра впис. и опис. сферы и их радиусов для облегчения изучения темы площади сферы и объема шара.

Программа требует знания: - терминов сферы, шара, цилиндра, конуса, впис и опис шара около призмы, пирамиды, цилиндра, конуса; - св-ва фигур, полученных при пересечении сферы и пл-ти (особое внимание касат. пл-ти), сф., цил., кон., пл-тью параллельной основаниям; - уметь решать з-чи на построение осевых сечений и сечений им параллельным.

Материал по объему не велик, но вводится много нов понятий (по теме сф. и шар - 34). Особенности методики: 1) введения назв. тела (уч-ся самост-но) и формулир. целей изучения; 2) введение опр.; 3) выделение и хар-ка сопутствующих эл-тов; 4) прав. вып-ние рисунка, исп-ние штампов, шаблонов для экономии времени; 5) max исп-ние наглядности.

Приведем пример реализации данной методики при введ. понятия сфера. Роль учителя состоит в организации поисковой деят-ти уч-ся в рез-те кот они сами сформулир. необх. опр. тел и назовут их эл-ты. Чтобы ввести понятие сферы нужно актуализировать знания уч-ся по окр-ти. Нарисов. на доске окр. попросить назв. эту фигуру, а затем разделить лист тетр. на 2 части и в лев. Сверху напис. – окр. Вызв. ученика к доске (ост. в тетр.) нарис. окр. и на ней отметить центр, радиус, диаметр, хорду, дать опр окр, сокращенное обознач. (w(O,r)), выделить полуокр. др. цветом. Показыв. уч-ся сферу (модель) (она м б из ниток, стеклян.) изображаем ее в прав. части тетради (предварительно написав сверху «сфера») и просим учен. назв. эл-ты сф. кот. имеют такое же назв. как в окр. Дополнит понятия: полюса, ось сф. и новое обознач.W. Опр. уч-ся формулир. сам-но. Особ-ти изображения: полюса – концы диаметра сф., но они не лежат на изображ окр.

После этого обратить внимание как наз. глава – Тела вращения. Можно ли установить в рез-те вращ. известн. вам геом фигуры или ее части получить сферу. Обратить внимание на рис слева и показать модель.

Опр. Сферой наз. пов-ть, образ-ая при повороте полуокр-ти с центром в т. О около диаметральной прямой на 360.

Затем можно перейти к рассм-нию св-в сферы исп-я метод аналогии с окр-тью. Вспомнить как могут располаг. по отнош. др. к др. окр-ть и прямая (9 кл) и повтор. все св-ва, опр., призн. касат. к прям., а затем сформулир. и док-тьанал. св-ва для сферы.

Св-ва. 1) сечение сф. пл-тью есть окр-ть; 2) касат. пл-ть перпенд. радиусу, провед. в т. касания; 3) если пл-ть перпенд. радиусу сф. и имеет с ней одну т., то она касается сферы (признак).

В мат-ке как в науке сфера (шар) имеют отдельные части (сегмент, пояс, слой, сектор), однако в наст.время не изуч.

После изучения теоретич. сведений о сф., ввод. понятия многогр. впис. и опис. около нее.

Методика введ понятий цилиндра и конуса в действующих уч. пособ. имеет свои особенности. Понятия их опред через поверхность, однако для учеников доступнее опред. этих фигур как тел получившихся в результате вращения плоских фигур (цилиндр - прямоугольника вокруг одной из сторон, конус - прямоугольного треугольника вокруг любого катета). В этом случае с научной точки зрения речь идет о прямом круговом цил., огранич. 2-мя параллельными пл-тями и кон., огранич. пл-тью. В связи с этим в пособ. Шл. как и в науке ввод понятия цилиндр. и конич. поверхностей.

В некоторой пл-ти α рассм окр-ть ω(0,R). Через каждую точку окр-ти ω(0,R) проведем прямую, перп-ную пл-ти α. Цилиндрической поверх-тью наз фигура, образованная этими прямыми, а сами прямые наз образующими цилиндрической пов-ти.

Прямым круговым цилиндром (цилиндром) наз. геом. тело, ограниченное цилиндр поверх-тью и двумя параллельными пл-тями α и β, кот перпендикулярны образующим цилиндр пов-ти.

После введ опр необх показать изображение цил-ра и попросить учеников подписать все эл-ты и дать им опр. Бок пов-тью цилиндра наз часть цилиндр пов-ти, расположенная м-ду секущими пл-ми α и β, кот перпендикулярны ее образующим, а часть (круги), отсекаемые цилиндр пов-тью на параллельных пл-тях α и β, наз основаниями цилиндра. Образующими цилиндра наз отрезки образующих цилинд пов-ти, расположенные м-ду параллельными пл-тями, в кот лежат основания цилиндра. Осью цилиндра наз отрезок О₁О₂,соединяющих центры О₁ и О₂ кругов, явл основаниями цилиндра.

Высотой цил-ра наз длина его образующей, а радиусом цил-ра наз радиус его основания. Осевым сечением цилиндра наз сечение цил-ра пл-тью, проходящей через его ось.

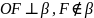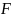Для введ. понятия конус ввод. понятие конич. пов-ти: 1.На некот. пл-ти рис окр-ть пров. прямую . 2.Через т. и каждую т-ку окр-ти проводят прямые. Фигуру образ этими прямыми наз конич. пов-тью, а прямые – образующими.

Опр. Конусом наз. геом. тело огранич. пов-тью и кругом с границей .

Аналог. ввод. понятие основания, высоты, оси, вершина, бок. пов-ть. Обратить внимание на изображ. его осевого сечения. К этому времени у уч-ся и у учителя д б модели эллипсов. Обязат. для изуч. явл. понятие усеч. конуса, как части конуса распол. м-ду его основанием и секущ. пл-тью перпендик. оси конуса.