2. Дифференцируемость функции в точке. Производная и дифференциал.

Задача Лейбница. Проведем секущую через М₀ и М, Δх=х-х₀, Δf(x)=f(x₀+Δx)-f(x₀)Будем приближать тМ к М₀ вдоль кривой Г(т. М-фиксир).

Секущая будет менять свое положение.

Опр. Предельное положение секущей ММ₀ наз касательной к кривой Г в т.х₀ при ММ. Найдем предельное положение секущей, выраж через унгол . К_{ММ 0}-угловой коэф-т секущей. К_{ММ 0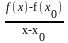}= =f(x₀)/x=tg, при хх₀  ММ₀

К- угловой коэф-т производной. К=limf(x₀)/x= tg, тогда уравнение касательной примет вид y=f(x₀)+K(x-x₀) x0

Опр. Производной ф-ции f(x) в предельной точке х₀ Д называется предел приращения ф-ции к вызвавшему это приращение аргумента, при стремлении последнего к нулю (f_x’(x₀)= limf(x₀)/x, x0).

Из задачи Лейбница вытекает геометрический смысл производной (производная есть tg угла наклона касательной к положительному направлению оси ОХ).

Опр. Ф-ция y=f(x) называется дифф-мой в точке х₀Д(f),если ее приращение можно представить в виде y=A*x+(x)x, где (x)-б/м при x0 (lim (x)=0), А-const, которая зависит от х.

Пример. Исследовать на дифф-ть ф-цию y=x³ в точке (0,0)

y=f(0+x)-f(0)=x³-0=0*x+x²*x, А=0, *x=x²0 при x0

Если f(x) имеет конечную производную в точке, то она дифф-ма в данной точке.

Критерий (дифф ф-ции в точке): Ф-ция y=f(x) называется дифф в точке х₀Д(f), когда она имеет в этой точке конечную производную.

Необходимость: y=A*x+(x)x, где (x)-б/м при x0

Разделим на x и перейдем к пределу при x0. Получим f_x’(x₀)=A+0=A конечная производная.

Достаточность: f_x’(x₀)=limy /x(x0)

y /x= f_x’(x₀)+(x) , где (x)-б/м при x0, тогда y = f_x’(x₀)х+(x) х,

(огр) (б/м) (б/м) (б/м)  при x0 y0 чтд.

(б/м)

Опр. Линейная однородная ф-ция вида f ’(x₀)х наз-ся дифф-лом ф-ции y=f(x) в точке х₀Д(f)

Теор: Пусть ф-ции u=g(x), дифф-я в точке х₀Д(g) и y=f(u), дифф-я в точке u₀Д(f),u₀=g(x₀). Тогда любая ф-ция y=f(g(x)) дифф-ма в т. х₀Д(g).

Теор: Пусть ф-ции y=f(x) определена и обратима в окрес точки х₀ и имеет в этой точке f’(x₀)0,а обратная ф-ция x=f^-1(y) непрерывна в точке y₀=f(x₀), тогда обратная ф-ция в точке y₀ имеет производную (f ^–1(y))’=1/ f ’(x₀).

(x^)’=x^-1, (a^x)’=a^xlna, (log _ax)’=1/(x*lna), (lnx)’=1/x, (sinx)’=cosx, (tgx)’=1/cos²x, (arcsinx)’=1/sqrt(1-x²), (arctgx)’=1/(1+x²).

2. Основные теоремы дифференциального исчисления.

Теор Ферма: Если ф-ция y=f(x) определена в окресности точки х₀, дифф-ма в самой этой точке и принимает в ней наибольшее или наименьшее значение, то производная в этой точке равна 0.

Док-во: пусть f(x₀)-наибольшее значение, возьмём хÛ_(х₀) f(x)f(x₀), f(x)- f(x₀)0. Рассмотрим отношения: f(x)-f(x₀) 0, x<x₀ По теореме о предельном переходе в нерав-вах получим, что lim (f(x)-f(x₀)) / x-x₀ 0(xx₀-0)

x-x₀ 0, x>x₀ lim (f(x)-f(x₀)) / x-x₀ 0(xx₀+0)

Т.к. ф-ция дифф-ма, то имеет конечную производную lim(f(x)-f(x₀) / x-x₀)=f ’(x₀) при xx₀

Тогда по Т(об односторон пределах) получаем, что левый предел= f ’(x₀), f ’(x₀) 0, правый предел = f ’(x₀), f ’(x₀)  0  f ’(x₀)=0 чтд.

Геометрический смысл т.Ферма: Если для ф-ции f(x) выполняется условие Т.Ферма, то в точке х₀ ф-ция имеет касательную, параллельную оси ОХ.

Теор Ролля: Если ф-ция y=f(x)

1. непрерывна на [a,b]

2. дифф-ма на (а,b)

3. f(a)=f(b), то  c(a,b), что f ’(c)=0

Геометрический смысл т. Ролля: Если для ф-ции f(x) выполняется условие т.Ферма , то между точками a и b найдется точка с, в которой касательная параллельна оси ОХ.

Теор Лагранжа: Если ф-ция y=f(x) непрерывна на [a,b], дифф-ма на (а,b), то  c(a,b), что f ’(c)= (1)

Геометрический смысл т. Лагранжа: =tg=:f ’(M)

Если для ф-ции f(x) выполняется условие т.Лагранжа, то на кривой f(x) найдется точка M(c, f(c)), касательная в которой параллельна хорде, соединяющей точки (a, f(a)) и (b,f(b)).

Теор Коши: Если ф-ции y₁=f(x) и y₂=g(x) непрерывны на [a,b], дифф-мы на (а,b), g’(x)0 x(a,b), то  c(a,b), что (2)

Замечание: Т.Лагранжа является частным случаем т.Коши и (1) получается из (2), если g(x)=x.